Question

15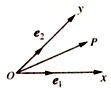．如图，设Ox、Oy是平面内相交成45°角的两条数轴，$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量，若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，则把有序数对（x，y）叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标，在此坐标系下，假设$\overrightarrow{OA}$=（-2，2$\sqrt{2}$），$\overrightarrow{OB}$=（2，0），$\overrightarrow{OC}$=（5，-3$\sqrt{2}$），则下列命题不正确的是（　　）

• A． $\overrightarrow{{e}_{1}}$=（1，0）
• B． |$\overrightarrow{OA}$|=2$\sqrt{3}$
• C． $\overrightarrow{OA}$∥$\overrightarrow{BC}$
• D． $\overrightarrow{OA}$⊥$\overrightarrow{OB}$

Answer 1

分析 利用定义判断A，根据余弦定理判断B，根据向量共线定理判定C，转化为正交分解判断D．

解答 解：$\overrightarrow{{e}_{1}}$=1×$\overrightarrow{{e}_{1}}$+0×$\overrightarrow{{e}_{1}}$，∴$\overrightarrow{{e}_{1}}$=（1，0）；故A正确；
由余弦定理可知|$\overrightarrow{OA}$|=$\sqrt{4+8-2×2×2\sqrt{2}×cos45°}$=2，故B错误；
∵$\overrightarrow{BC}$=$\overrightarrow{OC}-\overrightarrow{OB}$=（3，-3$\sqrt{2}$）=-$\frac{3}{2}$$\overrightarrow{OA}$，∴$\overrightarrow{OA}$∥$\overrightarrow{BC}$，故C正确；
$\overrightarrow{OA}$的直角坐标为（0，2），$\overrightarrow{OB}$的直角坐标系为（2，0），
∴$\overrightarrow{OA}⊥\overrightarrow{OB}$．故D正确．
故选B．

点评 本题考查了平面向量的基本定理，属于中档题．