题目内容
已知函数g(x)是幂函数,h(x)=ax-1,f(x)=h(x)-g(x),且函数f(x)的图象过点(4,-
)和(1,1)两点.
(1)求f(x)的解析式;
(2)求函数f(x)的单调区间,判断函数在区间[-2,3]上是否存在最大值或最小值;若存在,求出对应的最值;若不存在,说明理由.
| 7 |
| 2 |
(1)求f(x)的解析式;
(2)求函数f(x)的单调区间,判断函数在区间[-2,3]上是否存在最大值或最小值;若存在,求出对应的最值;若不存在,说明理由.
考点:函数的最值及其几何意义,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)将点(4,-
)代入函数f(x)=h(x)-g(x)的解析式,可得指数及a的值,进而得到f(x)的解析式;
(2)根据(1)中函数的解析式,分析函数的图象和性质,进而可得答案.
| 7 |
| 2 |
(2)根据(1)中函数的解析式,分析函数的图象和性质,进而可得答案.
解答:
解:(1)∵函数g(x)是幂函数,h(x)=ax-1,
∴设g(x)=xα,
∴f(x)=ax-1-xα,
又∵函数f(x)的图象过点(4,-
)和(1,1)两点.
∴
,
解得:a=2,α=1,
∴f(x)=
-x,
(2)∵f(x)=
-x的定义域为{x|x≠0},
又∵f′(x)=
<0恒成立,
故函数f(x)的单调递减区间为(-∞,0)和(0,+∞),
函数在区间[-2,3]上无最大值和最小值.
∴设g(x)=xα,
∴f(x)=ax-1-xα,
又∵函数f(x)的图象过点(4,-
| 7 |
| 2 |
∴
|
解得:a=2,α=1,
∴f(x)=
| 2 |
| x |
(2)∵f(x)=
| 2 |
| x |
又∵f′(x)=
| -x2-2 |
| x2 |
故函数f(x)的单调递减区间为(-∞,0)和(0,+∞),
函数在区间[-2,3]上无最大值和最小值.
点评:本题考查的知识点是函数解析式的求地,函数的单调性,函数的最值,是函数图象和性质的综合应用,难度中档.

练习册系列答案
相关题目
非零向量
,
满足
•
-2
2
2=0,|
|+|
|=1,则
与
的夹角的最小值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
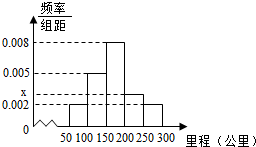 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.