题目内容
11.已知平面α、β和直线l1、l2,且α∩β=l2,且“l1∥l2”是“l1∥α,且l1∥β”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合线面平行的性质和判定进行求解即可.
解答 解:若α∩β=l2,则当l1∥l2时有可能l1?α或者l2?β,即充分性不成立,
反之若“l1∥α,且l1∥β”,则l1∥l2成立,即必要性成立,
即“l1∥l2”是“l1∥α,且l1∥β”的必要不充分条件,
故选:B.
点评 本题主要考查充分条件和必要条件的判断,结合线面平行的判定定理是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.六个人站成一排照相,要求甲、乙、丙3人有且只有两人相邻,则不同的站法种数有( )
| A. | 18 | B. | 108 | C. | 216 | D. | 432 |
16.下列4个命题中:
(1)?x0∈(0,+∞),使得2x0<3x0
(2)?x0∈(0,1),使得log2x0≥log3x0
(3)?x∈(0,+∞),log2x<2x
(4)?x∈(0,+∞),log2x<$\frac{1}{x}$
真命题的是( )
(1)?x0∈(0,+∞),使得2x0<3x0
(2)?x0∈(0,1),使得log2x0≥log3x0
(3)?x∈(0,+∞),log2x<2x
(4)?x∈(0,+∞),log2x<$\frac{1}{x}$
真命题的是( )
| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
3.函数y=xsinx(x∈[-π,π])的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
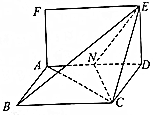 已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.
已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.