题目内容
2.设α、β、γ为平面,m、n、l为直线,则能推m⊥β是( )| A. | α⊥β,α∩β=l,m⊥l | B. | α∩γ=m,α⊥γ,β⊥γ | C. | α⊥γ,β⊥γ,m⊥α | D. | n⊥α,n⊥β,m⊥α |
分析 根据面面垂直的判定定理可知选项A是否正确,
根据平面α与平面β的位置关系进行判定可知选项B和C是否正确,
根据垂直于同一直线的两平面平行,以及与两平行平面中一个垂直则垂直于另一个平面,可知选项D正确
解答 解:对于A,α⊥β,α∩β=l,m⊥l,根据面面垂直的判定定理可知,缺少条件m?α,故不正确;
对于B,α∩γ=m,α⊥γ,β⊥γ,而α与β可能平行,也可能相交,则m与β不一定垂直,故不正确;
对于C,α⊥γ,β⊥γ,m⊥α,而α与β可能平行,也可能相交,则m与β不一定垂直,故不正确;
对于D,n⊥α,n⊥β,⇒α∥β,而m⊥α,则m⊥β,故正确;
故选:D.
点评 本小题主要考查空间线面关系、面面关系等知识,考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力,属于基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
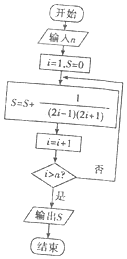
8.执行如图所示的程序框图,如果输入n=3,则输出的S值为( )

| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
10.一个几何体的三视图及尺寸如图所示,则该几何体的体积为( )


| A. | 24 | B. | 30 | C. | 48 | D. | 72 |
17.已知向量$\overrightarrow a•(\overrightarrow a+2\overrightarrow b)=0$,$|\overrightarrow a|=|\overrightarrow b|=2$,则向量$\overrightarrow a,\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
11.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,那么$|{3\overrightarrow a+\overrightarrow b}|$等于( )
| A. | 4 | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | $\sqrt{7}$ |
12.某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
(1)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(2)有多少的把握认为“学生的学习积极性与对待班级工作的态度”有关系?请说明理由.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 积极参加班级工作 | 不积极参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)有多少的把握认为“学生的学习积极性与对待班级工作的态度”有关系?请说明理由.
附:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |