题目内容
直线2x-3y+1=0和x-3=0的夹角是( )
A、π-arctan
| ||||
B、
| ||||
C、arctan
| ||||
D、
|
考点:两直线的夹角与到角问题
专题:直线与圆
分析:根据直线直线2x-3y+1=0的倾斜角为arctan
,直线x-3=0的斜角为90°,由此可得直线2x-3y+1=0和x-3=0的夹角.
| 2 |
| 3 |
解答:
解:由于直线直线2x-3y+1=0的斜率为
,故此直线的倾斜角为arctan
.
由于直线x-3=0的斜率不存在,斜角为90°,故直线2x-3y+1=0和x-3=0的夹角为
-arctan
,
故选:B.
| 2 |
| 3 |
| 2 |
| 3 |
由于直线x-3=0的斜率不存在,斜角为90°,故直线2x-3y+1=0和x-3=0的夹角为
| π |
| 2 |
| 2 |
| 3 |
故选:B.
点评:本题主要考查求直线的斜率和倾斜角,两条直线的夹角的定义,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
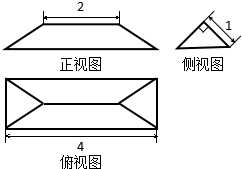 如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体体积为( )
如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
sin6,cos6,tan6,cos2中,大于0的是( )
| A、sin6 | B、cos6 |
| C、tan6 | D、cos2 |
已知一个几何体的三视图如图所示,则这个几何体的体积是( )


A、
| ||
B、
| ||
C、
| ||
D、
|