Question

设x、y满足约束条件

3x-y-6≤0 x-y+2≥0 x、y≥0

，若目标函数z=ax+by（a＞0，b＞0）的最大值为6，则

4

a

+

6

b

的最小值为（　　）

• A、

  25

  6

• B、

  25

  3

• C、

  50

  4

• D、

  50

  3

Answer 1

考点：简单线性规划的应用

专题：不等式的解法及应用

分析：由线性规划结合题意易得

2

3

a+b=1，从而

4

a

+

6

b

=（

4

a

+

6

b

）（

2

3

a+b）=

8

3

+6+

4b

a

+

4a

b

，由基本不等式可求．

解答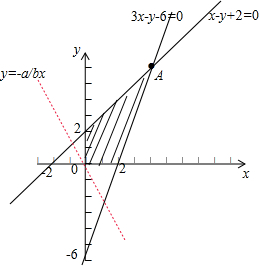： 解：作出约束条件

3x-y-6≤0 x-y+2≥0 x、y≥0

所对应的可行域（如图阴影），
目标函数可化为y=-

a

b

x+

1

b

z，（a＞0，b＞0），
联立

3x-y-6=0 x-y+2=0

可解得

x=4 y=6

，即A（4，6）
平移直线易得当直线经过点A（4，6）时，目标函数取最大值6，
代入数据可得4a+6b=6，即

2

3

a+b=1，
∴

4

a

+

6

b

=（

4

a

+

6

b

）（

2

3

a+b）=

8

3

+6+

4b

a

+

4a

b

≥

26

3

+2

4b a • 4a b

=

26

3

+2×4=

50

3

当且仅当

4b

a

=

4a

b

即a=b=

3

5

时，

4

a

+

6

b

取到最小值

50

3

，
故选：D

点评：本题考查线性规划和基本不等式的综合应用，准确作图并变形为可利用基本不等式的情形是解决问题的关键，属中档题．