题目内容
19.已知函数f(x)=sinωx-cosωx(ω>0)的最小正周期为π.(1)求函数y=f(x)图象的对称轴方程;
(2)讨论函数f(x)在$[0,\frac{π}{2}]$上的单调性.
分析 (1)利用辅助角公式化简函数的解析式,根据正弦函数的周期性求得ω,可得其解析式,利用正弦函数的图象的对称求得函数y=f(x)图象的对称轴方程.
(2)利用正弦函数的单调性求得函数f(x)在$[0,\frac{π}{2}]$上的单调性.
解答 解:(1)∵$f(x)=sinωx-cosωx=\sqrt{2}sin(ωx-\frac{π}{4})$,且T=π,∴ω=2.
于是$f(x)=\sqrt{2}sin(2x-\frac{π}{4})$,令$2x-\frac{π}{4}=kπ+\frac{π}{2}$,得$x=\frac{kπ}{2}+\frac{3π}{8}(k∈Z)$,
即函数f(x)的对称轴方程为$x=\frac{kπ}{2}+\frac{3π}{8}(k∈Z)$.
(2)令$2kπ-\frac{π}{2}≤2x-\frac{π}{4}≤2kπ+\frac{π}{2}$,得函数f(x)的单调增区间为$[kπ-\frac{π}{8},kπ+\frac{3π}{8}](k∈Z)$.
注意到$x∈[0,\frac{π}{2}]$,令k=0,
得函数f(x)在$[0,\frac{π}{2}]$上的单调增区间为$[0,\frac{3π}{8}]$;
同理,求得其单调减区间为$[\frac{3π}{8},\frac{π}{2}]$.
点评 本题主要考查辅助角公式,正弦函数的周期性、单调性、以及它的图象的对称性,属于基础题.

练习册系列答案
相关题目
10.直线l:y=k(x+$\sqrt{2}$)与曲线C:x2-y2=1(x<0)相交于P,Q两点,则直线l的倾斜角的取值范围是( )
| A. | ($\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{3π}{4}$) | B. | ($\frac{π}{4}$,$\frac{3π}{4}$) | C. | (0,$\frac{π}{2}$)∪($\frac{π}{2}$,π) | D. | [0,π) |
7.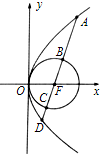 如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )
如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )
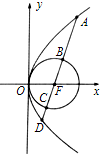 如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )
如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
14.已知函数$f(x)={sin^4}x+{cos^4}x,x∈[-\frac{π}{4},\frac{π}{4}]$,若f(x1)<f(x2),则一定有( )
| A. | x1<x2 | B. | x1>x2 | C. | ${x_1}^2<{x_2}^2$ | D. | ${x_1}^2>{x_2}^2$ |
2.已知命题p:“?x∈R,使”4x+2x+1-m=0”,若“¬p”为假命题,则实数m的取值范围是( )
| A. | (-1,+∞) | B. | (0,+∞) | C. | [0,+∞) | D. | [1,+∞) |



