题目内容
在△ABC中,最大角A为最小角C的2倍,且三边a,b,c为三个连续整数,求a,b,c的值.
考点:余弦定理
专题:解三角形
分析:根据三角函数的边角关系,设出a,b,c,利用正弦定理和余弦定理建立方程关系解方程即可得到结论.
解答:
解:∵最大角A为最小角C的2倍,且三边a,b,c为三个连续整数,
∴A>B>C,即a>b>c,
不妨设a=n+1,b=n,c=n-1,n≥2.
由正弦定理得
=
,
则
=
=
,
即cosC=
,
由余弦定理得cosC=
=
=
=
,
即
=
,
解得n=5,则a=6,b=5,c=4.
∴A>B>C,即a>b>c,
不妨设a=n+1,b=n,c=n-1,n≥2.
由正弦定理得
| a |
| sinA |
| c |
| sinC |
则
| n+1 |
| sin2C |
| n-1 |
| sinC |
| n+1 |
| 2sinCcosC |
即cosC=
| n+1 |
| 2(n-1) |
由余弦定理得cosC=
| a2+b2-c2 |
| 2ab |
| (n+1)2+n2-(n-1)2 |
| 2n(n+1) |
| n+4 |
| 2(n+1) |
| n+1 |
| 2(n-1) |
即
| n+4 |
| n+1 |
| n+1 |
| n-1 |
解得n=5,则a=6,b=5,c=4.
点评:本题主要考查解三角形的应用,利用正弦定理和余弦定理,建立方程组是解决本题的关键.

练习册系列答案
相关题目
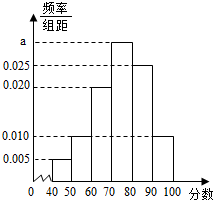 为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.