题目内容
14.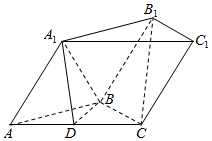 如图,三棱柱ABC-A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.
如图,三棱柱ABC-A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.(Ⅰ)求证:B1C∥平面A1BD;
(Ⅱ)若∠A1AB=∠ACB=60°,AB=BB1,AC=2,BC=1,求三棱锥A1-ABD的体积.
分析 (1)连接AB1,交A1B于点O,连接DO,根据线面平行的判定定理即可证明B1C∥平面A1BD;
(2)若∠A1AB=∠ACB=60°,AB=BB1,AC=2,BC=1,分别求出三棱锥的底面积和高的大小,根据三棱锥的体积公式即可求三棱锥A1-ABD的体积.
解答 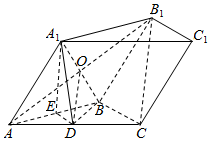 (1)连接AB1,交A1B于点O,连接DO
(1)连接AB1,交A1B于点O,连接DO
在△ACB1中,点D是AC的中点,点O是AB1的中点
∴CB1∥DO,
∵BC1?平面A1BD,DO?平面A1BD
∴BC1∥平面A1BD.
(2)取AB的中点E,连接A1E,ED,
则ED∥BC,且ED=$\frac{1}{2}$BC=$\frac{1}{2}×1$=$\frac{1}{2}$,
∵∠A1AB=60°,AB=BB1,
∴四边形AA1B1B是菱形,
则AE⊥AB,∵平面AA1B1B⊥平面ABC,
∴AE⊥平面ABC,
即AE是三棱锥A1-ABD的高,
∵∠ACB=60°,AC=2,BC=1,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}-2AC•BCcos60°}$=$\sqrt{4+1-2×2×1×\frac{1}{2}}$=$\sqrt{3}$,
则满足AC2=BC2+AB2,
即△ABC是直角三角形,
则BC⊥AB,即ED⊥AB,
则△ABD的面积S△ABD=$\frac{1}{2}AB•ED$=$\frac{1}{2}×\sqrt{3}×\frac{1}{2}$=$\frac{\sqrt{3}}{4}$,
AE=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$
则三棱锥A1-ABD的体积V=$\frac{1}{3}$S△ABD•AE=$\frac{1}{3}×$$\frac{\sqrt{3}}{4}$×$\frac{3}{2}$=$\frac{\sqrt{3}}{8}$.
点评 本题主要考查线面平行的判定以及三棱锥体积的计算,根据面面垂直和线面平行的性质定理求出三棱锥的底面积和高是解决本题的关键.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案| A. | 32 | B. | 42 | C. | 46 | D. | 56 |
| A. | $\frac{5}{4}$x2-5y2=1 | B. | 5y2-$\frac{5}{4}$x2=1 | C. | $\frac{5}{4}$y2-5x2=1 | D. | 5x2-$\frac{5}{4}$y2=1 |
| A. | 2x+y=0 | B. | 2x+y=1 | C. | x+2y=0 | D. | x+2y=1 |
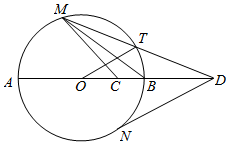 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT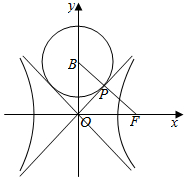 如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.
如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.