题目内容
2.抛物线y2=16x的焦点到双曲线$\frac{x^2}{12}-\frac{y^2}{4}=1$渐近线的距离为2.分析 先求出抛物线y2=16x的焦点,再求出双曲线$\frac{x^2}{12}-\frac{y^2}{4}=1$的渐进线,由此利用点到直线的距离公式能求出抛物线y2=16x的焦点到双曲线$\frac{x^2}{12}-\frac{y^2}{4}=1$渐近线的距离.
解答 解:抛物线y2=16x的焦点(4,0),
双曲线$\frac{x^2}{12}-\frac{y^2}{4}=1$的渐进线:$x±\sqrt{3}y=0$,
∴抛物线y2=16x的焦点到双曲线$\frac{x^2}{12}-\frac{y^2}{4}=1$渐近线的距离为:
d=$\frac{4}{2}=2$.
故答案为:2.
点评 本题考查抛物线的焦点到双曲线的渐近线的距离的求法,是中档题,解题时要认真审题,注意点到直线的距离公式、抛物线、双曲线的性质的合理运用.

练习册系列答案
相关题目
15.集合A={x∈N|-1<x<4}的真子集个数为( )
| A. | 7 | B. | 8 | C. | 15 | D. | 16 |
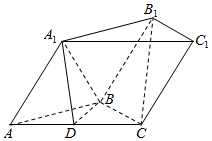 如图,三棱柱ABC-A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.
如图,三棱柱ABC-A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.