题目内容

下列各选项中，与sin2013°最接近的数是（　　）
A、-
1
2
B、
1
2
C、
2
2
D、-
2
2
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：2013°=6×360°-157°，利用诱导公式判断即可．
解答： 解：sin2013°=sin（6×360°-157°）=-sin157°，
又-sin150°=-
1
2
，
∴与sin2013°最接近的数是-
1
2
，
故选：A．
点评：本题考查运用诱导公式化简求值，属于基础题．
练习册系列答案
相关题目
对于实数对（a，b）和（c，d），规定：（a，b）=（c，d）当且仅当a=c，c=d，定义运算如下：
①（a，b）?（c，d）=（ac-bd，bc+ad）；
②（a，b）⊕（c，d）=（a+c，b+d）．
设p，q∈R，若（1，2）?（p，q）=（5，0），则（1，2）⊕（p，q）等于（　　）
A、（4，0）
B、（2，0）
C、（0，2）
D、（0，4）
掷一枚质地均匀的硬币3次，恰有2次正面向上的概率为（　　）
A、
2
3
B、
3
8
C、
1
3
D、
1
2
下列命题正确的个数是（　　）
①若直线与平面有两个公共点，则直线在平面内；
②若直线l上有无数个点不在平面α内，则l∥α；
③若直线l与平面α相交，则直线l与平面α内的任意直线都是异面直线；
④若平面α∥平面β，直线a?α，直线b?β，则直线a∥b；
⑤若直线l与平面α不平行，则直线l与平面α有公共点；
⑥如果两条异面直线中的一条与一个平面平行，则另一条直线一定与该平面相交．
A、1个B、2个C、3个D、4个
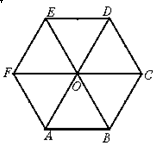如图，设O是正六边形ABCDEF的中心，在向量
OB
，
OC
，
OD
，
OE
，
OF
，
AB
，
BC
，
CD
，
EF
，
DE
，
FA
中与
OA
共线的向量有（　　）
A、1个B、2个C、3个D、4个
cos2
π
12
-sin2
π
12
=（　　）
A、
1
2
B、-
1
2
C、-
3
2
D、
3
2
已知直线l1：x+sinθ•y-1=0，l2：cosθ•x+
1
2
y+1=0，其中0≤θ≤
π
2
．
（1）若l1⊥l2，求tanθ的值；
（2）求直线l1的倾斜角a的取值范围．
设f（x）=log 
1
2
1-ax
x-1
为奇函数，a为常数，
（1）求a的值；
（2）证明f（x）在区间（1，+∞）上单调递减；
（3）若x∈[3，4]，不等式f（x）＞（
1
2
）x+m恒成立，求实数m的取值范围．
设数列{an}的前n项和为Sn，a1=1，an=
Sn
n
+2（n-1）（n∈N*）．
（1）求证：数列{an}为等差数列，并分别写出an和Sn关于n的表达式；
（2）设数列{
1
an•an+1
}的前n项和为Tn，证明：
1
5
≤Tn＜
1
4
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网