题目内容
19.已知函数f(x)=$\left\{{\begin{array}{l}{{x^2}-1,x≥0}\\{-2x,x<0}\end{array}}$,则关于x的方程f[f(x)]+k=0给出下列四个命题:①存在实数k,使得方程恰有1个实根;
②存在实数k,使得方程恰有2个不相等的实根;
③存在实数k,使得方程恰有3个不相等的实根;
④存在实数k,使得方程恰有4个不相等的实根.
其中正确命题的序号是①②③(把所有满足要求的命题序号都填上).
分析 由解析式判断出f(x)的正负,再求出f[f(x)]的解析式,根据指数函数的图象画出此函数的图象,根据方程根的几何意义和图象,判断出方程根的个数以及对应的k的范围,便可以判断出命题的真假.
解答 解:当∈[0,1)时,f(x)<0,当∈(-∞,0)∪[1,+∞)时,f(x)>0,
∴f[f(x)]=$\left\{\begin{array}{l}{4{x}^{2}-1,(x<0)}\\{{x}^{4}-2{x}^{2},(x≥1)}\\{-2{x}^{2}+2,(0≤x<1)}\end{array}\right.$,
画出此函数的图象如下图:
∵f[f(x)]+k=0,∴f[f(x)]=-k,
由图得,当-1<-k<0时,方程恰有1个实根;
当-k>2或-k=0时,方程恰有2个实根,当0<-k≤2时,方程恰有3个实根,
故①②③正确.
故答案为:①②③.
点评 本题考查了命题的真假判断,以及方程根的根数问题,涉及到了分段函数求值,指数函数的图象及性质应用,考查了学生作图能力和转化思想.

练习册系列答案
相关题目
10.△ABC满足下列条件:①b=3,c=4,B=30°;②a=5,b=8,A=30°;③c=6,b=3$\sqrt{3}$,B=60°;④c=9,b=12,C=60°.其中有两个解的是( )
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ③④ |
7.若α,β为锐角,tan(α+β)=3,$tanβ=\frac{1}{2}$,则α的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
11.已知抛物线C:y2=8x,点P为抛物线上任意一点,过点P向圆D:x2+y2-4x+3=0作切线,切点分别为A,B,则四边形PADB面积的最小值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
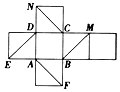 如图是正方体的平面展开图.关于这个正方体,有以下判断:①EC⊥平面AFN;
如图是正方体的平面展开图.关于这个正方体,有以下判断:①EC⊥平面AFN;