题目内容
2．已知$cos（\frac{π}{6}+x）=\frac{1}{3}$，则$cos（\frac{5π}{6}-x）$的值为（ ）| A． | $\frac{1}{3}$ | B． | $-\frac{1}{3}$ | C． | $-\frac{{2\sqrt{2}}}{3}$ | D． | $\frac{{2\sqrt{2}}}{3}$ |
分析 根据诱导公式化简可求值．
解答 解：由$cos（\frac{5π}{6}-x）$=cos（π-$\frac{π}{6}$-x）=-cos（$\frac{π}{6}$+x）
∵$cos（\frac{π}{6}+x）=\frac{1}{3}$，
∴$cos（\frac{5π}{6}-x）$=-$\frac{1}{3}$．
故选B．
点评 本题主要考查了诱导公式的化解能力．属于基本知识的考查．
练习册系列答案
相关题目
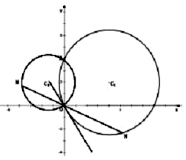已知圆${C_1}：{（{x-4}）^2}+{（{y-2}）^2}=20$与y轴交于O，A两点，圆C2过O，A两点，且直线C2O与圆C1相切；
10．函数y=|tan x|的周期为（ ）
| A． | $\frac{π}{2}$ | B． | Π | C． | 2π | D． | 3π |
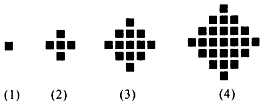某民族的刺绣有着悠久的历史，如图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮．先按照同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形．
7．已知复数z1=-2-i，z2=i，i是虚数单位，则复数z1-2z2的值是（ ）
| A． | -1+2i | B． | 1-2i | C． | 1+2i | D． | -2-3i |
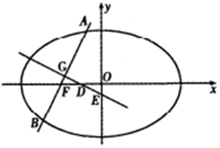如图，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F（-c，0），过点F的直线交椭圆于A，B两点，当直线AB经过椭圆的一个顶点时，其倾斜角恰为60°．
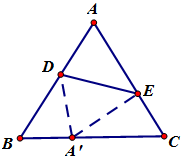在△ABC中，a，b，c分别为内角A，B，C所对的边，且满足$\frac{tanA}{tanB}=\frac{2c-b}{b}$．
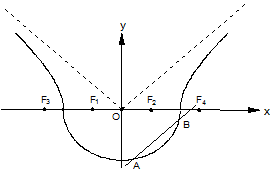如图，曲线Г由曲线C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0，y≤0）和曲线C2：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0，y＞0）组成，其中点F1，F2为曲线C1所在圆锥曲线的焦点，点F3，F4为曲线C2所在圆锥曲线的焦点，