��Ŀ����
 Ϊ�˽�ס��������IJ�Ʒ�������ֱ�����������IJ�Ʒ�и������ȡ10����������Ʒ��ij��Ԫ�صĺ�������λ�����ˣ�����������ݵľ�Ҷͼ��ͼ���涨������Ʒ�д���Ԫ�غ�������18����ʱ���϶��ò�ƷΪ�ŵ�Ʒ��
Ϊ�˽�ס��������IJ�Ʒ�������ֱ�����������IJ�Ʒ�и������ȡ10����������Ʒ��ij��Ԫ�صĺ�������λ�����ˣ�����������ݵľ�Ҷͼ��ͼ���涨������Ʒ�д���Ԫ�غ�������18����ʱ���϶��ò�ƷΪ�ŵ�Ʒ����1���ԱȽϼס������������IJ�Ʒ�и���Ԫ�غ�����ƽ��ֵ�Ĵ�С��
��2���ִ��ҳ�����ķ��ŵ�Ʒ�������ȡ�����������ٳ鵽һ����Ԫ�غ���Ϊ10���˻�13���˵IJ�Ʒ�ĸ��ʣ�
���㣺�оٷ���������¼������¼������ĸ���,��Ҷͼ
ר�⣺������ͳ��
��������1�����ݾ�Ҷͼ��֪ʶ����ƽ�����Ķ��壬���ƽ�����Ƚϼ��ɣ�
��2���Ǻ���Ϊ10��13���˵�����ΪA��B������������Ʒ�ֱ�ΪC��D��E��F������������Ʒ�������ȡ����������15�������С����ٳ鵽һ������Ϊ10���˻�13���˵IJ�Ʒ������ɵĻ����¼���9�������ݸ��ʹ�ʽ���㼴��
��2���Ǻ���Ϊ10��13���˵�����ΪA��B������������Ʒ�ֱ�ΪC��D��E��F������������Ʒ�������ȡ����������15�������С����ٳ鵽һ������Ϊ10���˻�13���˵IJ�Ʒ������ɵĻ����¼���9�������ݸ��ʹ�ʽ���㼴��
���
�⣺��1���׳�ƽ��ֵΪ
��9+18+15+16+19+13+23+20+25+21��=17.9��
�ҳ�ƽ��ֵΪ
��18+14+15+16+19+10+13+21+20+23��=16.9��
���Լ׳�ƽ��ֵ�����ҳ�ƽ��ֵ
��2���Ǻ���Ϊ10��13���˵�����ΪA��B������������Ʒ�ֱ�ΪC��D��E��F������������Ʒ�������ȡ�������������¼��У�AB��AC��AD��AE��AF��BC��BD��BE��BF��CD��CE��CF��DE��DF��EF����15����
�����ٳ鵽һ������Ϊ10���˻�13���˵IJ�Ʒ������ɵĻ����¼��У�AB��AC��AD��AE��AF��BC��BD��BE��BF����9����
���������P=
=
| 1 |
| 10 |
�ҳ�ƽ��ֵΪ
| 1 |
| 10 |
���Լ׳�ƽ��ֵ�����ҳ�ƽ��ֵ
��2���Ǻ���Ϊ10��13���˵�����ΪA��B������������Ʒ�ֱ�ΪC��D��E��F������������Ʒ�������ȡ�������������¼��У�AB��AC��AD��AE��AF��BC��BD��BE��BF��CD��CE��CF��DE��DF��EF����15����
�����ٳ鵽һ������Ϊ10���˻�13���˵IJ�Ʒ������ɵĻ����¼��У�AB��AC��AD��AE��AF��BC��BD��BE��BF����9����
���������P=
| 9 |
| 15 |
| 3 |
| 5 |
���������⿼���˾�Ҷͼ��֪ʶ�Լ��ȿ����¼��ĸ��ʣ��ؼ���һһ�оٳ����еĻ����¼������ڻ�����

��ϰ��ϵ�д�
�����Ŀ
��֪����P={x|��x-3����x-6����0��x��Z}��Q={5��7}�����н��۳������ǣ�������
| A��Q⊆P |
| B��P��Q=P |
| C��P��Q=Q |
| D��P��Q={5} |
Բx2+y2-2y-1=0����ֱ��x-2y-3=0�ԳƵ�Բ�����ǣ�������
A����x-2��2+��y+3��2=
| ||
| B����x-2��2+��y+3��2=2 | ||
C����x+2��2+��y-3��2=
| ||
| D����x+2��2+��y-3��2=2 |
���⡰��x��a2+b2����x��2ab�����������ǣ�������
| A������x��a2+b2����x��2ab�� |
| B������x��a2+b2����x��2ab�� |
| C������x��2ab����x��a2+b2�� |
| D������x��a2+b2����x��2ab�� |
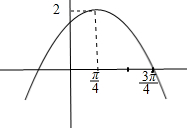 ��֪����f��x��=2sin����x+�գ����أ�0��|��|��
��֪����f��x��=2sin����x+�գ����أ�0��|��|��