题目内容
如图,在底面为平行四边形的四棱锥P-ABCD中,E,F分别是棱AD、BP上的动点,且满足AE=2BF,则线段EF中点的轨迹是( )


| A、一条直线 |
| B、一段圆弧 |
| C、抛物线的一部分 |
| D、一个平行四边形 |
考点:轨迹方程,棱柱的结构特征
专题:空间位置关系与距离
分析:设EF的中点是0,取AB中点M,作EG平行于AB交BC于G,连结FG,取GF中点N,根据AE=2BF,判断中点O满足的关系式,即可得到结论.
解答:
解:设EF的中点是0,取AB中点M,作EG平行于AB交BC于G,连结FG,取GF中点N,则OMBN为平行四边形,
从而MO∥BN.作CH∥GF于H,取CH中点K.
因为AE=2BF,所以BG=2BF,而∠CBP 是确定的角,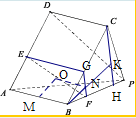
故△BGF与△BCH 相似,从而N在BK上.
所以O在平行于直线BK的一条直线上.
故选:A
从而MO∥BN.作CH∥GF于H,取CH中点K.
因为AE=2BF,所以BG=2BF,而∠CBP 是确定的角,

故△BGF与△BCH 相似,从而N在BK上.
所以O在平行于直线BK的一条直线上.
故选:A
点评:本题主要考查空间直线的位置关系的判断,根据AE=2BF,利用辅助线,建立中点满足的关系是解决本题的关键.考查学生的空间想象和推理能力.

练习册系列答案
相关题目
下面是2×2列联表:
则a+b+c等于( )
| y1 | y2 | 总计 | |
| x1 | a | b | 73 |
| x2 | 22 | c | 47 |
| 总计 | 74 | 46 | 120 |
| A、96 | B、97 | C、99 | D、98 |
下列命题中,错误的是( )
| A、平行于同一平面的两个平面平行 |
| B、垂直于同一个平面的两个平面平行 |
| C、若a,b是异面直线,则经过直线a与直线b平行的平面有且只有一个 |
| D、若一个平面与两个平行平面相交,则交线平行 |
下列函数中,周期为π且为偶函数的是( )
A、y=cos(2x-
| ||
B、y=sin(2x+
| ||
C、y=sin(x+
| ||
| D、y=cos(x+π) |
已知函数y=f(x)为R上可导函数,且对?x∈R都有f(2x)=x3f′(1)-10x成立,则函数y=f(x),x∈[-1,1]的值域为( )
| A、R | B、[-6,6] |
| C、[0,6] | D、(-∞,0) |