题目内容
3.求函数f(x)=lnx+ln(1-x)+x的单调区间.分析 先确定f(x)的定义域,在对f(x)求导,即可找出单调区间.
解答 解:∵f(x)=ln x+ln(1-x)+x,
∴定义域为(0,1),
f′(x)=$\frac{{x}^{2}+x-1}{x(x-1)}$,
令f′(x)=0,解得x=$\frac{\sqrt{5}-1}{2}$,
∵在区间(0,1)上,由f′(x)>0可得,x<$\frac{\sqrt{5}-1}{2}$成立,由f′(x)<0可得,x>$\frac{\sqrt{5}-1}{2}$成立
又0<$\frac{\sqrt{5}-1}{2}$<1
∴f(x)的递增区间是(0,$\frac{\sqrt{5}-1}{2}$)递减区间是($\frac{\sqrt{5}-1}{2}$,1).
点评 本题关键是求出定义域,熟练求导,解出单调性区间.

练习册系列答案
相关题目
13.若函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$)的图象关于直线x=$\frac{π}{12}$对称,且当x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}$),x1≠x2时,f(x1)=(x2),则f(x1+x2)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
18.(-$\sqrt{x}$+$\frac{1}{x}$)10的展开式中x2的系数等于( )
| A. | 45 | B. | 20 | C. | -30 | D. | -90 |
10.已知某圆柱的体积为V,若要使其表面积的值小其底面半径应为( )
| A. | $\root{3}{V}$ | B. | $\root{3}{\frac{V}{π}}$ | C. | $\root{3}{4V}$ | D. | $\root{3}{\frac{V}{2π}}$ |
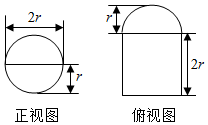 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图 中的正视图和俯视图如图所示,若 该几何体的表面积为64+80π,则 r=( )
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图 中的正视图和俯视图如图所示,若 该几何体的表面积为64+80π,则 r=( )