题目内容
12．
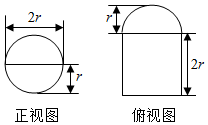圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体的三视图 中的正视图和俯视图如图所示，若 该几何体的表面积为64+80π，则 r=（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 8 |
分析 几何体为半圆柱与半球的组合体．
解答 解：由俯视图可知几何体为半圆柱与半球的组合体，半圆柱与半球的半径均为r，半圆柱的高为2r，
∴几何体的表面积为为$\frac{1}{2}×4π{r}^{2}$+$\frac{1}{2}π{r}^{2}$+$\frac{1}{2}π{r}^{2}$+πr×2r+2r×2r=5πr2+4r2=64+80π．
解得r=4．
故选：C．
点评 本题考查了空间几何体的三视图，圆柱的结构特征，面积计算，属于基础题．
练习册系列答案
相关题目
17．函数y=f（x）在（0，2）上是增函数，函数y=f（x+2）是偶函数，则下列结论正确的是（ ）
| A． | f（1）＜f（$\frac{5}{2}$）＜f（$\frac{7}{2}$） | B． | f（$\frac{5}{2}$）＜f（1）＜f（$\frac{7}{2}$） | C． | f（$\frac{7}{2}$）＜f（$\frac{5}{2}$）＜f（1） | D． | f（$\frac{7}{2}$）＜f（1）＜f（$\frac{5}{2}$） |
4．已知定义域为R的函数f（x）满足f（-x）=-f（x+4），且当x＞2时，f（x）单调递增．如果x1+x2＜4，且（x1-2）（x2-2）＜0，则f（x1）+f（x2）的取值范围是（ ）
| A． | （-∞，0） | B． | （-∞，0] | C． | （0，1] | D． | （0，+∞） |
1．在△ABC中，$\overrightarrow{AB}=\overrightarrow c，\overrightarrow{BC}=\overrightarrow a，\overrightarrow{CA}=\overrightarrow b$，下列推导不正确的是（ ）
| A． | 若$\overrightarrow a•\overrightarrow b＞0$，则△ABC为钝角三角形 | B． | $\overrightarrow a•\overrightarrow b=0$，则△ABC为直角三角形 | ||
| C． | $\overrightarrow a•\overrightarrow b=\overrightarrow b•\overrightarrow c$，则△ABC为等腰三角形 | D． | $\overrightarrow c•（{\overrightarrow a+\overrightarrow b+\overrightarrow c}）=0$，则△ABC为正三角形 |