题目内容
在△ABC中，BC=
，AC=3，sinC=2sinA．
（Ⅰ）求AB的值．
（Ⅱ）求sin2A的值．
| 5 |
（Ⅰ）求AB的值．
（Ⅱ）求sin2A的值．
考点：正弦定理
专题：计算题,三角函数的求值,解三角形
分析：（Ⅰ）由正弦定理将角化为边，计算即可得到；
（Ⅱ）由余弦定理可得cosA，再由平方关系可得sinA，再由二倍角的正弦公式计算即可得到．
（Ⅱ）由余弦定理可得cosA，再由平方关系可得sinA，再由二倍角的正弦公式计算即可得到．
解答：
解：（Ⅰ）由正弦定理可得，
sinC=2sinA，
即为AB=2BC=2
；
（Ⅱ）由余弦定理可得，
cosA=
=
=
，
即有sinA=
=
，
则有sin2A=2sinAcosA=2×
×
=
．
sinC=2sinA，
即为AB=2BC=2
| 5 |
（Ⅱ）由余弦定理可得，
cosA=
| AB2+AC2-BC2 |
| 2AB•AC |
| 20+9-5 | ||
2×2
|
| 2 | ||
|
即有sinA=
1-
|
| 1 | ||
|
则有sin2A=2sinAcosA=2×
| 1 | ||
|
| 2 | ||
|
| 4 |
| 5 |
点评：本题考查正弦定理和余弦定理及运用，考查同角的平方关系和二倍角的正弦公式的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
某商店一个月的收支数据为a1，a2，…aN，按程序框图进行统计，那么关于S，T的关系正确的是（ ）
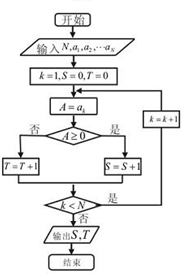
| A、N=S-T | B、N=S+T |
| C、S≥T | D、S≤T |
下列推断错误的是（ ）
| A、命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1则x2-3x+2≠0” |
| B、命题p：存在x0∈R，使得x02+x0+1＜0，则非p：任意x∈R，都有x2+x+1≥0 |
| C、若p且q为假命题，则p，q均为假命题 |
| D、“x＜1”是“x2-3x+2＞0”的充分不必要条件 |
若函数f（x）=sinωx（ω＞0）在[
，
]上是单调函数，则ω应满足的条件是（ ）
| π |
| 6 |
| π |
| 2 |
| A、0＜ω≤1 |
| B、ω≥1 |
| C、0＜ω≤1或ω=3 |
| D、0＜ω≤3 |
若函数f（x）=
则f（log54）=（ ）
|
A、
| ||
| B、3 | ||
C、
| ||
| D、4 |
已知等差数列{an}满足a2+a8=4，a3+a11=8，则它的前11项之和等于（ ）
| A、22 | B、33 | C、44 | D、66 |