题目内容
12.若不等式x2-ax+1≥0对一切x∈(0,1]恒成立,则a的取值范围是(-∞,2].分析 由题意可得a≤x+$\frac{1}{x}$对一切x∈(0,1]恒成立,由f(x)=x+$\frac{1}{x}$在(0,1]递减,可得f(x)的最小值,即可得到a的范围.
解答 解:不等式x2-ax+1≥0对一切x∈(0,1]恒成立,
即有a≤x+$\frac{1}{x}$对一切x∈(0,1]恒成立,
由f(x)=x+$\frac{1}{x}$≥2,当且仅当x=1时取得最小值,在(0,1]递减,
可得x=1时,可得f(x)取得最小值,且为2.
则有a≤2.
故答案为:(-∞,2].
点评 本题考查二次不等式恒成立问题的解法,注意运用参数分离和函数的单调性,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{10}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | 3 |
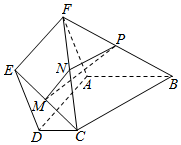 如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.
如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.