Question

如图，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF∥AB，EF=

3

2

，EF与面AC的距离为2，则该多面体的体积为

 

．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：分别取AB、CD的中点G、H，连EG，GH，EH，把该多面体分割成一个四棱锥E-AGHD与一个三棱柱EGH-FBC，由此能求出该面体的体积．

解答： 解：分别取AB、CD的中点G、H，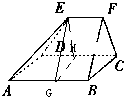
连EG，GH，EH，
把该多面体分割成一个四棱锥E-AGHD与一个三棱柱EGH-FBC，
∵面ABCD是边长为3的正方形，EF∥AB，
EF=

3

2

，EF与面AC的距离为2，
∴S_{四边形AGHD}=3×

3

2

=

9

2

，S_△EGH=

1

2

×3×2=3，
∴四棱锥E-AGHD的体积为V₁=

1

3

×2×

9

2

=3，
三棱柱EGH-FBC的体积V₂=

3

2

×3=

9

2

，
∴整个多面体的体积为V=V₁+V₂=3+

9

2

=

15

2

．

点评：本题考查多面体的体积的求法，解题时要认真审题，注意空间思维能力的培养．