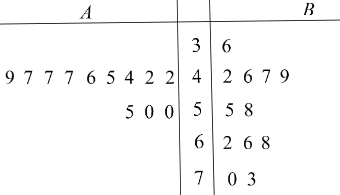
题目内容
16．已知x＞0，y＞0，x+y+$\sqrt{xy}$=2，则x+y的取值范围是[$\frac{4}{3}$，2）．分析 根据基本不等式的性质求出x+y的范围即可．
解答 解：∵x＞0，y＞0，x+y+$\sqrt{xy}$=2，
∴2-（x+y）=$\sqrt{xy}$≤$\frac{x+y}{2}$，
∴$\frac{3}{2}$（x+y）≥2，
∴x+y≥$\frac{4}{3}$，
故答案为：[$\frac{4}{3}$，2）．
点评 本题考查了基本不等式的性质，考查转化思想，是一道基础题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
7．设向量$\overrightarrow a$，$\overrightarrow b$满足|${\overrightarrow a$-$\overrightarrow b}$|=2$\sqrt{3}$，|${\overrightarrow a$+$\overrightarrow b}$|=2，则$\overrightarrow a$•$\overrightarrow b$=（ ）
| A． | $2\sqrt{3}$ | B． | $-2\sqrt{3}$ | C． | -2 | D． | 2 |
4．某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个）．经过2个小时，这种细菌由1个可繁殖成（ ）
| A． | 512个 | B． | 256个 | C． | 128个 | D． | 64个 |
1．下列说法正确是（ ）
| A． | 常数列一定是等比数列 | B． | 常数列一定是等差数列 | ||
| C． | 等比数列一定不是摆动数列 | D． | 等差数列可能是摆动数列 |
