题目内容
7.设向量$\overrightarrow a$,$\overrightarrow b$满足|${\overrightarrow a$-$\overrightarrow b}$|=2$\sqrt{3}$,|${\overrightarrow a$+$\overrightarrow b}$|=2,则$\overrightarrow a$•$\overrightarrow b$=( )| A. | $2\sqrt{3}$ | B. | $-2\sqrt{3}$ | C. | -2 | D. | 2 |
分析 将等式进行平方,相减即可得到结论.
解答 解:∵|${\overrightarrow a$-$\overrightarrow b}$|=2$\sqrt{3}$,|${\overrightarrow a$+$\overrightarrow b}$|=2,
∴|${\overrightarrow a$-$\overrightarrow b}$|2=|${\overrightarrow a$|2+|$\overrightarrow b}$|2-2${\overrightarrow a$•$\overrightarrow b}$=12,
|${\overrightarrow a$+$\overrightarrow b}$|2=|${\overrightarrow a$|2+|$\overrightarrow b}$|2+2${\overrightarrow a$•$\overrightarrow b}$=4,
∴4${\overrightarrow a$•$\overrightarrow b}$=-8,
∴${\overrightarrow a$•$\overrightarrow b}$=-2,
故选:C.
点评 本题主要考查向量的基本运算,利用平方进行相减是解决本题的关键,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若实数x,y满足不等式组:$\left\{{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{3x-y-3≤0}\end{array}}\right.$,则该约束条件所围成的平面区域的面积是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
19.已知i是虚数单位,则复数z1=2-i,z2=1+2i,则z1•z2在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
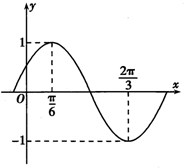 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.