题目内容
5.已知等差数列{an}满足:a3=10,a7=26.(1)求数列{an}的通项公式;
(2)请问88是数列{an}中的项吗?若是,请指出它是哪一项;若不是,请说明理由.
分析 (1)利用等差数列通项公式解出即可得出.
(2)令88=an=4n-2.解得n即可判断出结论.
解答 解:(1)设等差数列{an}的公差为d,∵a3=10,a7=26.
∴a1+2d=10,a1+6d=26,
联立解得a1=2,d=4.
∴an=2+4(n-1)=4n-2.
(2)令88=an=4n-2.解得n=$\frac{45}{2}$∉N*,
所以88不是数列{an}中的项.
点评 本题考查了等差数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.下列函数既是奇函数又在区间(0,+∞)上为增函数的是( )
| A. | y=sinx,x∈R | B. | y=x2,x∈R | C. | y=x-$\frac{1}{x}$,x≠0 | D. | y=2-x,x∈R |
10.(x-2)5的展开式中,二项式系数的最大值为( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
15.如果用$\overline{A}$表示随机事件A的对立事件,若事件A表示“汽车甲畅销且汽车乙滞销”,则事件$\overline{A}$表示( )
| A. | 汽车甲、乙都畅销 | B. | 汽车甲滞销或汽车乙畅销 | ||
| C. | 汽车甲滞销 | D. | 汽车甲滞销且汽车乙畅销 |
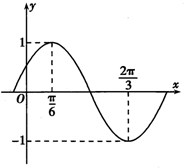 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.