题目内容
若函数y=
在(m,+∞)上为增函数(m为常数),则称f(x)为区间(m,+∞)上的“一阶比增函数”,(m,+∞)为f(x)的一阶比增区间.
(1)若f(x)=xlnx-2ax2是(0,+∞)上的“一阶比增函数”,求实数a的取值范围;
(2)若f(x)=λx3-xlnx-x2 (λ>0,λ为常数),且g(x)=
有唯一的零点,求f(x)的“一阶比增区间”;
(3)若f(x)是(0,+∞)上的“一阶比增函数”,求证:?x1,x2∈(0,+∞),f(x1)+f(x2)<f(x1+x2).
| f(x) |
| x |
(1)若f(x)=xlnx-2ax2是(0,+∞)上的“一阶比增函数”,求实数a的取值范围;
(2)若f(x)=λx3-xlnx-x2 (λ>0,λ为常数),且g(x)=
| f(x) |
| x |
(3)若f(x)是(0,+∞)上的“一阶比增函数”,求证:?x1,x2∈(0,+∞),f(x1)+f(x2)<f(x1+x2).
考点:函数单调性的性质
专题:函数的性质及应用
分析:(1)利用“一阶比增函数”的意义,利用导数和函数单调性之间的关系即可得出;
(2)利用“一阶比增函数”的意义,利用g(x)=
有唯一的零点先求出λ的值,即可得到f(x)的“一阶比增区间”;
(3)利用“一阶比增函数”的意义及增函数的定义即可证明;
(2)利用“一阶比增函数”的意义,利用g(x)=
| f(x) |
| x |
(3)利用“一阶比增函数”的意义及增函数的定义即可证明;
解答:
解:(1)若f(x)=xlnx-2ax2是(0,+∞)上的“一阶比增函数”,
则y=
=lnx-2ax,
则y'=
-2a,
要使f(x)=xlnx-2ax2是(0,+∞)上的“一阶比增函数”,
则y'=
-2a≥0恒成立,即a≤
恒成立,
∵x>0,
∴a≤0.
(2)若f(x)=λx3-xlnx-x2 (λ>0,λ为常数),
则g(x)=
=λx2-lnx-x,
由g(x)=
=λx2-lnx-x=0,
得λx2-x=lnx,
设y=λx2-x和y=lnx,
要使g(x)=
有唯一的零点,则由y=λx2-x和y=lnx的图象可知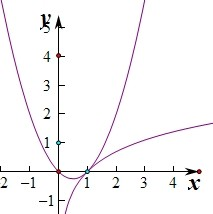
当y=λx2-x经过点(1,0)时,函数g(x)=
有唯一的零点,
此时λ-1=0,解得λ=1,
此时g(x)=
=x2-lnx-x,
g'(x)=2x-1-
=
,
由g'(x)=
>0,
得2x2-x-1>0,
∴x>1或x<-
(舍去),
即函数g(x)的单调区间为(1,+∞),
∴f(x)的“一阶比增区间”是(1,+∞);
(3)∵f(x)是“一阶比增函数”,即
在(0,+∞)上是增函数,
又?x1,x2∈(0,+∞),有x1<x1+x2,x2<x1+x2,
∴
<
,
<
,
即f(x1)<
,f(x2)<
∴f(x1)+f(x2)<
+
=f(x1+x2).
∴?x1,x2∈(0,+∞),f(x1)+f(x2)<f(x1+x2)成立.
则y=
| f(x) |
| x |
则y'=
| 1 |
| x |
要使f(x)=xlnx-2ax2是(0,+∞)上的“一阶比增函数”,
则y'=
| 1 |
| x |
| 1 |
| 2x |
∵x>0,
∴a≤0.
(2)若f(x)=λx3-xlnx-x2 (λ>0,λ为常数),
则g(x)=
| f(x) |
| x |
由g(x)=
| f(x) |
| x |
得λx2-x=lnx,
设y=λx2-x和y=lnx,
要使g(x)=
| f(x) |
| x |

当y=λx2-x经过点(1,0)时,函数g(x)=
| f(x) |
| x |
此时λ-1=0,解得λ=1,
此时g(x)=
| f(x) |
| x |
g'(x)=2x-1-
| 1 |
| x |
| 2x2-x-1 |
| x |
由g'(x)=
| 2x2-x-1 |
| x |
得2x2-x-1>0,
∴x>1或x<-
| 1 |
| 2 |
即函数g(x)的单调区间为(1,+∞),
∴f(x)的“一阶比增区间”是(1,+∞);
(3)∵f(x)是“一阶比增函数”,即
| f(x) |
| x |
又?x1,x2∈(0,+∞),有x1<x1+x2,x2<x1+x2,
∴
| f(x1) |
| x1 |
| f(x1+x2) |
| x1+x2 |
| f(x2) |
| x2 |
| f(x1+x2) |
| x1+x2 |
即f(x1)<
| x1f(x1+x2) |
| x1+x2 |
| x2f(x1+x2) |
| x1+x2 |
∴f(x1)+f(x2)<
| x1f(x1+x2) |
| x1+x2 |
| x2f(x1+x2) |
| x1+x2 |
∴?x1,x2∈(0,+∞),f(x1)+f(x2)<f(x1+x2)成立.
点评:本题主要考查函数单调性的应用,正确“一阶比增函数”的意义及增函数的定义及利用已经证明过的结论是解题的关键.涉及的知识点较多,综合性较强.

练习册系列答案
相关题目
设a,b,c均为正数,且a+
=1,b+lgb=3,c+2c=4,则( )
| a |
| A、a<c<b |
| B、a<b<c |
| C、c<a<b |
| D、c<b<a请解释 |
设集合P={x|0≤x≤2},Q={y|0≤y≤2},给出如下6个图形,其中能表示从集合P到集合Q的函数关系的有( )


| A、2个 | B、3个 | C、4个 | D、5个 |
 某市对排污水进行综合治理,征收污水处理费,系统对各厂一个月内排出的污水量m吨收取的污水处理费y元,运行程序如下所示:
某市对排污水进行综合治理,征收污水处理费,系统对各厂一个月内排出的污水量m吨收取的污水处理费y元,运行程序如下所示: