题目内容
已知△ABC中，内角A，B，C的对边分别为a，b，c，且cos2B=3cos（A+C）+1．
（1）求B；
（2）若cosA=
，△abc的面积为
，求△ABC的外接圆的面积．
（1）求B；
（2）若cosA=
| 4 |
| 5 |
36+9
| ||
| 50 |
考点：正弦定理的应用
专题：解三角形
分析：（Ⅰ）由条件可得 2cos2B+cosB-1=0，求得cosB的值，可得B的值．
（Ⅱ）由sinA=3sinC利用正弦定理可得a=3c，再根据△ABC的面积为
acsinB=
，求得ab值，再由正弦定理求得面积的值．
（Ⅱ）由sinA=3sinC利用正弦定理可得a=3c，再根据△ABC的面积为
| 1 |
| 2 |
36+9
| ||
| 50 |
解答：
解：（1）由题意，2cos2B-1=-3cosB+1⇒（cosB+2）（2cosB-1）=0，
∴cosB=
，B=
，
S△ABC=
=
absin(A+
)，
∵cosA=
，∴sinA=
，
∴sin（A+
）=
×
+
×
=
，
∴ab=
．
∴
=4R2=
=4⇒R=1．
∴S=πR2=π．
∴cosB=
| 1 |
| 2 |
| π |
| 3 |
S△ABC=
36+9
| ||
| 50 |
| 1 |
| 2 |
| π |
| 3 |
∵cosA=
| 4 |
| 5 |
| 3 |
| 5 |
∴sin（A+
| π |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
3+4
| ||
| 10 |
∴ab=
6
| ||
| 5 |
∴
| ab |
| sinAsinB |
| ||||||
|
∴S=πR2=π．
点评：本题主要考查二倍角公式、诱导公式、正弦定理的应用，
练习册系列答案
相关题目
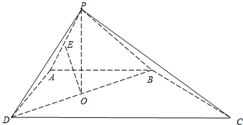如图，四棱锥P-ABCD的底面是直角梯形，AB∥CD，AB⊥AD，△PAB和△PAD是两个边长为2的正三角形，DC=4，O为BD的中点，E为PA的中点．
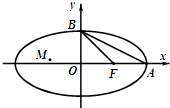如图，椭圆C：