题目内容
已知点M是椭圆C:
+
=1(a>b>0)上一点,F1,F2分别为C的左右焦点,|F1F2|=2
,∠F1MF2=60°,△F1MF2的面积为
.
(1)求椭圆C的方程;
(2)设过椭圆右焦点F2的直线l和椭圆交于两点A,B,是否存在直线l,使得△OAF2与△OBF2的面积比值为2?若存在,求出直线l的方程;若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 3 |
(1)求椭圆C的方程;
(2)设过椭圆右焦点F2的直线l和椭圆交于两点A,B,是否存在直线l,使得△OAF2与△OBF2的面积比值为2?若存在,求出直线l的方程;若不存在,说明理由.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:本题(1)利用正弦面积公式、余弦定理得到|MF1|、|MF2|的和,从而求出参数a、b、c,得到椭圆的方程;(2)将条件中的面积比转化为向量关系,得到两点纵坐关系,再通过直线和椭圆联列的方程组,得到两点的纵坐标关系,从而求出参数k,得到直线l的方程,说明其存在性.
解答:
解:(1)在△F1MF2中,S△F1MF2=
|MF1||MF2|sin60°=
,
得到:|MF1||MF2|=
.
由余弦定理,得|F1F2|2=|MF1|2+|MF2|2-2|MF1||MF2|COS60°.
=(|MF1|+|MF2|)2-2|MF1||MF2|(1+COS60°),
∴|MF1|+|MF2|=4.
∴2a=|MF1|+|MF2|=4,即a=2,b2=a2-c2=1.
故椭圆方程为
+y2=1.
(2)∵△OAF2与△OBF2的面积比值为2,
∴AF2:BF2=2,则
=2
,
设A(x1,y1),B(x2,y2),
则(
-x1,-y1)=2(x2-
,y2),
∴y1=-2y2 ①
设直线l的方程为x=ky+
.
由
,得到(k2+4)y2+2
y-1=0,
则y1+y2=-
②
y1y2=-
③
由①②③得k=±
,
因此存在直线l:x=±
y+
使得△OAF2与△OBF2的面积比值为2.
| 1 |
| 2 |
| ||
| 3 |
得到:|MF1||MF2|=
| 4 |
| 3 |
由余弦定理,得|F1F2|2=|MF1|2+|MF2|2-2|MF1||MF2|COS60°.
=(|MF1|+|MF2|)2-2|MF1||MF2|(1+COS60°),
∴|MF1|+|MF2|=4.
∴2a=|MF1|+|MF2|=4,即a=2,b2=a2-c2=1.
故椭圆方程为
| x2 |
| 4 |
(2)∵△OAF2与△OBF2的面积比值为2,
∴AF2:BF2=2,则
| AF2 |
| F2B |
设A(x1,y1),B(x2,y2),
则(
| 3 |
| 3 |
∴y1=-2y2 ①
设直线l的方程为x=ky+
| 3 |
由
|
| 3 |
则y1+y2=-
2
| ||
| k2+4 |
y1y2=-
| 1 |
| k2+4 |
由①②③得k=±
2
| ||
| 23 |
因此存在直线l:x=±
2
| ||
| 23 |
| 3 |
点评:本题考查了正弦面积公式、余弦定理、椭圆的定义、韦达定理,以及化归转化的数学思想,有一定的探索性,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 如图,三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为2的正三角形,且∠BAC=90°,O、D分别为BC、AB的中点.
如图,三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为2的正三角形,且∠BAC=90°,O、D分别为BC、AB的中点.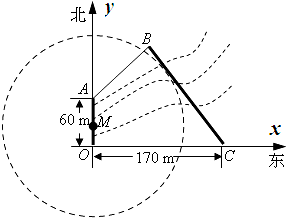 如图:为了保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸).规划要求:新桥BC与河岸AB垂直,保护区的边界为圆心M(在线段OA上)与BC相切的圆.建立如图所示的直角坐标系,已知新桥BC所在直线的方程为:4x+3y-680=0.
如图:为了保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸).规划要求:新桥BC与河岸AB垂直,保护区的边界为圆心M(在线段OA上)与BC相切的圆.建立如图所示的直角坐标系,已知新桥BC所在直线的方程为:4x+3y-680=0.