题目内容

7．已知点A（0，2），抛物线C：y2=mx（m＞0）的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，若|FM|：|MN|=1：2，则△OFN的面积为（　　）
A．$8\sqrt{3}$B．$4\sqrt{3}$C．$\frac{8\sqrt{3}}{3}$D．$\frac{4\sqrt{3}}{3}$

分析 作出M在准线上的射影K，根据|KM|：|MN|确定|KN|：|KM|的值，进而列方程求得m，再由三角形的面积公式，计算即可得到所求值．

解答 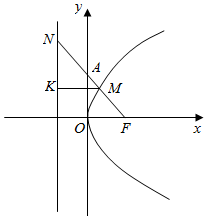解：抛物线C：y2=mx的焦点F（$\frac{m}{4}$，0）
设M在准线上的射影为K，
由抛物线的定义知|MF|=|MK|，
由|FM|：|MN|=1：2，可得|KM|：|MN|=1：2，
则|KN|：|KM|=$\sqrt{3}$：1，kFN=-$\sqrt{3}$
kFN=$\frac{0-2}{\frac{m}{4}-0}$=-$\frac{8}{m}$，
即有$\frac{8}{m}$=$\sqrt{3}$，求得m=$\frac{8\sqrt{3}}{3}$，
则三角形OFN的面积为$\frac{1}{2}$•yN•|OF|=$\frac{1}{2}$×2×$\frac{4\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$．
故选D．

点评 本题主要考查了抛物线的简单性质．抛物线中涉及焦半径的问题常利用抛物线的定义转化为点到准线的距离来解决．

练习册系列答案
相关题目
17．已知函数f（x）=exsinx-cosx，g（x）=xcosx-$\sqrt{2}$ex，（其中e是自然对数的底数）．
（1）?x1∈[0，$\frac{π}{2}$]，?x2∈[0，$\frac{π}{2}$]使得不等式f（x1）+g（x2）≥m成立，试求实数m的取值范围；
（2）若x＞-1，求证：f（x）-g（x）＞0．
18．如图，在四棱锥P-ABCD中，E是PC的中点，底面ABCD为矩形，AB=4，AD=2，PA=PD，且平面PAD⊥平面ABCD，平面ABE与棱PD交于点F，平面PCD与平面PAB交于直线l．
（1）求证：l∥EF；
（2）求PB与平面ABCD所成角的正弦值为$\frac{2\sqrt{21}}{21}$，求二面角P-AE-B的余弦值．
15．设偶函数y=2sin（ωx+φ）（ω＞0，0＜φ＜π）的图象与直线y=2的某两个交点的横坐标分别为x1，x2，若|x2-x1||的最小值为π，则该函数在下列哪个区间上单调递增（　　）
A．（0，$\frac{π}{2}$）B．（-$\frac{π}{4}$，$\frac{π}{4}$）C．（-$\frac{π}{2}$，-$\frac{π}{4}$）D．（$\frac{π}{4}$，$\frac{3π}{4}$）
2．已知离心率为$\frac{1}{2}$的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点M（2，0），过点Q（1，0）的直线与椭圆C相交于A，B两点，设点P（4，3），记PA，PB的斜率分别为k1，k2
（Ⅰ）求椭圆C的方程；
（Ⅱ）探讨k1+k2是否为定值？如果是，求出该定值，如果不是，求出k1+k2的取值范围．
12．已知长方形ABCD如图1中，AD=$\sqrt{3}$，AB=2，E为AB中点，将△ADE沿DE折起到△PDE，所得四棱锥P-BCDE如图2所示．

（Ⅰ）若点M为PC中点，求证：BM∥平面PDE；
（Ⅱ）当平面PDE⊥平面BCDE时，求三棱锥E-PCD的体积．
19．已知复数z满足iz=1-i，则$\overline z$=（　　）
A．-1-iB．1-iC．-1+iD．1+i
16．在直角坐标系xOy中，直线$l：\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$（t为参数，$α∈（0，\frac{π}{2}）$）与圆C：x2+y2-2x-4x+1=0相交于点A，B，以O为极点，x轴正半轴为极轴建立极坐标系．
（1）求直线l与圆C的极坐标方程；
（2）求$\frac{1}{{|{OA}|}}+\frac{1}{{|{OB}|}}$的最大值．
17．在极坐标系中，极点到直线ρcosθ=1的距离为1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网