题目内容
15.已知等差数列{an}的前n项和为Sn,若S13=-26,a9=4,求:(1)数列{an}的通项公式;
(2)S8.
分析 (1)由题意可得S13=13a7=-26,可得a7,可得公差,进而可得通项;
(2)根据等差数列的求和公式计算即可
解答 解:(1)由题意可得S13=$\frac{13}{2}$(a1+a13)=13a7=-26,
解之可得a7=-2,故公差d=$\frac{{a}_{9}-{a}_{7}}{9-7}$=3,
故可得an=a9+(n-9)d=3n-23;
(2)由(1)可得a1=-20,
S8=8×(-20)+$\frac{8(8-1)}{2}$×3=-76.
点评 本题考查等差数列的前n项和,求出数列的通项是解决问题的关键,属基础题.

练习册系列答案
相关题目
3.在△ABC中,$B=\frac{π}{3},AC=\sqrt{3}$,则△ABC周长的取值范围是( )
| A. | $(2,3\sqrt{3}]$ | B. | $(2\sqrt{3},3\sqrt{3}]$ | C. | $[2,3\sqrt{3}]$ | D. | $(2\sqrt{3},3+\sqrt{3}]$ |
7.为了调查胃病是否与生活规律有关,在某地对540名40岁以上的人进行了调查,结果是:患胃病者生活不规律的共60人,患胃病者生活规律的共20人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共200人.
(1)根据以上数据列出2×2列联表;
(2)在犯错误的概率不超过0.01的前提下认为40岁以上的人患胃病与否和生活规律有关系吗?为什么?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d
(1)根据以上数据列出2×2列联表;
(2)在犯错误的概率不超过0.01的前提下认为40岁以上的人患胃病与否和生活规律有关系吗?为什么?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5.泰华中学采取分层抽样的方法从高二学生中按照性别抽出20名学生作为样本,其选报文科与理科的情况如下表所示:
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为泰华中学的高二学生选报文理科与性别有关?
注:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 男 | 女 | |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为泰华中学的高二学生选报文理科与性别有关?
注:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
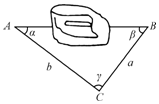 如图,某人为了测量某建筑物两侧A.B间的距离(在A,B处相互看不到对方),选定了一个可看到A、B两点的C点进行测量,你认为测量时应测量的数据是a,b,γ.
如图,某人为了测量某建筑物两侧A.B间的距离(在A,B处相互看不到对方),选定了一个可看到A、B两点的C点进行测量,你认为测量时应测量的数据是a,b,γ.