题目内容
17．
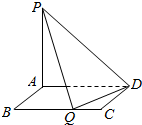如图所示，矩形ABCD的边AB=m，BC=4，PA⊥平面ABCD，PA=3，现有数据：①$m=\frac{3}{2}$；②m=3；③m=4；④$m=\sqrt{5}$．若在BC边上存在点Q（Q不在端点B、C处），使PQ⊥QD，则m可以取（ ）
| A． | ①② | B． | ①②③ | C． | ②④ | D． | ① |
分析 根据三垂线定理结合PQ⊥QD，可得PQ在底面的射影AQ也与QD垂直，由此可得平面ABCD内满足条件的Q点应在以AD为直径的圆上，得出m≤2，即可选出正确选项．
解答 
解：连接AQ，
因为PQ⊥QD，根据三垂线定理可得AQ⊥QD
在平面ABCD内，直径所对的圆周角为直角
所以Q点在以AD为直径的圆上，
故当BC与以AD为直径的圆有公共点时，在BC边上存在点Q，使PQ⊥QD
因此AB≤$\frac{1}{2}$AD=2，即m≤2
故选：D．
点评 本题考查了空间的直线与平面、直线与直线的位置关系，属于中档题．充分利用三垂线定理和平面内点的轨迹，是解决本题的关键所在．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
7．已知定义在R上的函数y=f（x）满足：函数y=f（x-1）的图象关于直线x=1对称，且当x∈（-∞，0），f（x）+xf′（x）＜0（f′（x）是函数f（x）的导函数）成立．若$a=（sin\frac{1}{2}）•f（sin\frac{1}{2}）$，b=（ln2）•$f（ln2），c=（lo{g_{\frac{1}{2}}}\frac{1}{4}）•$$f（lo{g_{\frac{1}{2}}}\frac{1}{4}）$，则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞a＞b | D． | a＞c＞b |
5．下列说法正确的是（ ）
| A． | 合情推理和演绎推理的结果都是正确的 | |
| B． | 若事件A，B是互斥事件，则A，B是对立事件 | |
| C． | 若事件A，B是对立事件，则A，B是互斥事件 | |
| D． | “复数z=a+bi（a，b∈R）是纯虚数”是“a=0”的必要不充分条件 |