题目内容
12.已知椭圆x2+2y2=4,则以(1,1)为中点的弦的长度为$\frac{\sqrt{30}}{3}$.分析 设弦的两端的端点为(a,b)和(2-a,2-b),列方程组$\left\{\begin{array}{l}{{a}^{2}+2{b}^{2}=4}\\{(2-a)^{2}+2(2-b)^{2}=4}\end{array}\right.$得两端点的坐标,由此可知弦长.
解答 解:设弦的两端的端点为(a,b)和(2-a,2-b)
列方程组$\left\{\begin{array}{l}{{a}^{2}+2{b}^{2}=4}\\{(2-a)^{2}+2(2-b)^{2}=4}\end{array}\right.$
解得a=1+$\frac{\sqrt{6}}{3}$,b=1-$\frac{\sqrt{6}}{6}$或a=1-$\frac{\sqrt{6}}{3}$,b=1+$\frac{\sqrt{6}}{6}$
两端点的坐标为(1-$\frac{\sqrt{6}}{3}$,1+$\frac{\sqrt{6}}{6}$)和(1+$\frac{\sqrt{6}}{3}$,1-$\frac{\sqrt{6}}{6}$)
弦长为$\sqrt{(\frac{2\sqrt{6}}{3})^{2}+(-\frac{2\sqrt{6}}{6})^{2}}$=$\frac{\sqrt{30}}{3}$.
故答案为:$\frac{\sqrt{30}}{3}$.
点评 本题考查直线的圆锥曲线的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
2. 如图,圆柱内有一个直三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形.如果三棱柱的体积为$12\sqrt{3}$,圆柱的底面直径与母线长相等,则圆柱的侧面积为( )
如图,圆柱内有一个直三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形.如果三棱柱的体积为$12\sqrt{3}$,圆柱的底面直径与母线长相等,则圆柱的侧面积为( )
 如图,圆柱内有一个直三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形.如果三棱柱的体积为$12\sqrt{3}$,圆柱的底面直径与母线长相等,则圆柱的侧面积为( )
如图,圆柱内有一个直三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形.如果三棱柱的体积为$12\sqrt{3}$,圆柱的底面直径与母线长相等,则圆柱的侧面积为( )| A. | 12π | B. | 14π | C. | 16π | D. | 18π |
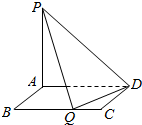 如图所示,矩形ABCD的边AB=m,BC=4,PA⊥平面ABCD,PA=3,现有数据:
如图所示,矩形ABCD的边AB=m,BC=4,PA⊥平面ABCD,PA=3,现有数据: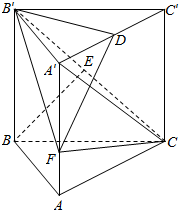 如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.