题目内容
6．关于x的不等式ax2-2ax+1≥0的解集为R，则实数a的取值范围为[0，1]．分析 对a分类讨论，利用一元二次不等式的解集与△的关系即可得出．
解答 解：a≠0时，由题意得$\left\{\begin{array}{l}{a＞0}\\{△≤0}\end{array}\right.$，
即$\left\{\begin{array}{l}{a＞0}\\{{4a}^{2}-4a≤0}\end{array}\right.$，
解得0＜a≤1；
当a=0时，恒有1≥0，不等式也成立；
综上所述，a的取值范围是[0，1]．
故答案为：[0，1]．
点评 本题考查了分类讨论思想和一元二次不等式的解集与判别式关系的应用问题，是基础题目．
练习册系列答案
相关题目
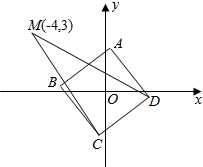如图所示，ABCD是以原点O为中心、边长为2的正方形，M点坐标为（-4，3），当正方形在满足上述条件下转动时，$\overrightarrow{MC}•\overrightarrow{MD}$的取值范围是[15，35]．
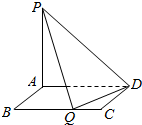如图所示，矩形ABCD的边AB=m，BC=4，PA⊥平面ABCD，PA=3，现有数据：