题目内容
9.设f(x)=$\left\{\begin{array}{l}{1,x>0}\\{0,x=0}\\{-1,x<0}\end{array}\right.$,g(x)=$\left\{\begin{array}{l}{1,x为有理数}\\{0,x为无理数}\end{array}\right.$,若f(g(a))=0,则( )| A. | a为无理数 | B. | a为有理数 | C. | a=0 | D. | a=1 |
分析 由f(x)=$\left\{\begin{array}{l}{1,x>0}\\{0,x=0}\\{-1,x<0}\end{array}\right.$可知g(a)=0,再由g(x)求得.
解答 解:∵f(g(a))=0,
∴g(a)=0,
∴a为无理数,
故选:A.
点评 本题考查了分段函数及复合函数的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.从某企业的某种产品中抽取n件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
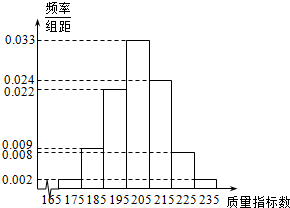
其中第二小组的频数为36,则n为( )

其中第二小组的频数为36,则n为( )
| A. | 200 | B. | 400 | C. | 2000 | D. | 4000 |
20.执行如图所示的程序框图若输出的n=9,则输入的整数p的最小值是( )


| A. | 50 | B. | 77 | C. | 78 | D. | 306 |
17.若将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{3}$个单位长度后得到函数g(x)的图象,则函数g(x)的解析式为( )
| A. | g(x)=sin(2x+$\frac{5π}{12}$) | B. | g(x)=sin(2x+$\frac{π}{12}$) | C. | g(x)=sin(2x-$\frac{π}{12}$) | D. | g(x)=sin(2x-$\frac{5π}{12}$) |
1.若复数z=$\frac{1-2i}{i}$的共轭复数是$\overline{z}$=a+bi(a,b∈R),其中i为虚数单位,则点(a,b)为( )
| A. | (-1.2) | B. | (-2,1) | C. | (1,-2) | D. | (2,-1) |
18.已知圆x2+y2-2x-4y+a-6=0上有且仅有两个点到直线3x-4y-15=0的距离为1,则实数a的取值范围是( )
| A. | (-6,7) | B. | (-15,1) | C. | (-14,2) | D. | (-8,1) |