题目内容
17.若将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{3}$个单位长度后得到函数g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=sin(2x+$\frac{5π}{12}$) | B. | g(x)=sin(2x+$\frac{π}{12}$) | C. | g(x)=sin(2x-$\frac{π}{12}$) | D. | g(x)=sin(2x-$\frac{5π}{12}$) |
分析 由条件利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{3}$个单位长度后,
得到函数g(x)=sin[2(x-$\frac{π}{3}$)+$\frac{π}{4}$]=sin(2x-$\frac{5π}{12}$)的图象,
故选:D.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
7.某程序框图如图所示,则该程序运行后输出的值等于( )
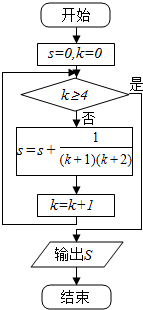

| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
2.已知sin α-3cos α=0,则$\frac{sin2α}{co{s}^2α-si{n}^2α}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
9.设f(x)=$\left\{\begin{array}{l}{1,x>0}\\{0,x=0}\\{-1,x<0}\end{array}\right.$,g(x)=$\left\{\begin{array}{l}{1,x为有理数}\\{0,x为无理数}\end{array}\right.$,若f(g(a))=0,则( )
| A. | a为无理数 | B. | a为有理数 | C. | a=0 | D. | a=1 |
6.已知命题p:y=sin(2x+$\frac{π}{3}$)的图象关于(-$\frac{π}{6}$,0)对称;命题q:若2a<2b,则lga<lgb.则下列命题中正确的是( )
| A. | p∧q | B. | ?p∧q | C. | p∧?q | D. | ?p∨q |
7.已知数列{an}的前n项和Sn=2n(n∈N*),则n≥2时,a12+a22+…+an2=( )
| A. | $\frac{1}{3}({4^n}-1)$ | B. | $\frac{1}{3}({4^n}+8)$ | C. | $\frac{1}{3}{({2^n}-1)^2}$ | D. | $\frac{1}{3}{({2^n}+4)^2}$ |