题目内容
7.已知函数f(x)=1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$,g(x)=1-x$+\frac{{x}^{2}}{2}$$-\frac{{x}^{3}}{3}$,设函数F(x)=f(x)•g(x),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b-a的最小值为3.分析 求出函数f(x)的导数,求出f(x)的单调区间,从而求出f(x)零点的范围,;通过讨论x的范围,求出g(x)在R的导数,得到g(x)的单调区间,从而求出g(x)所在的零点的范围,F ( x) 的零点均在区间[a,b],进而求出a,b的值,求出答案即可.
解答 解:∵f′(x)=1-x+x2>0,∴f(x)在R单调递增,而f(0)=1>0,f(-1)<0,
∴函数f(x)在区间(-1,0)内有零点;
又∵g′(x)=-1+x-x2<0,∴f(x)在R单调递减,而g(1)=1>0,g(2)=<0,
∴函数g(x)在区间(1,2)内有零点,
函数F(x)=f(x)?g(x),且函数 F ( x) 的零点在区间(-1,2)内,
则 b-a 的最小值为:3
故答案为:3
点评 本题考查函数的单调性的应用,函数的零点的求法,考查转化思想以及计算能力.属于中档题.

练习册系列答案
相关题目
5.在区间[-1,0]上任取两实数x、y,则y<3x的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
2.(1-x)5(1+$\sqrt{x}$)2的展开式中x4的系数为( )
| A. | -10 | B. | -5 | C. | 10 | D. | 15 |
12.已知f(x+y)=f(x)-f(y)对全体实数x,y都成立,则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
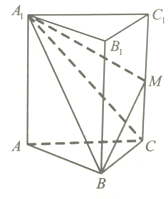 如图,在直三棱柱中ABC-A1B1C1中,二面角A-A1B-C是直二面角,AB=BC═2,点M是棱CC1的中点,三棱锥M-BCA1的体积为1.
如图,在直三棱柱中ABC-A1B1C1中,二面角A-A1B-C是直二面角,AB=BC═2,点M是棱CC1的中点,三棱锥M-BCA1的体积为1.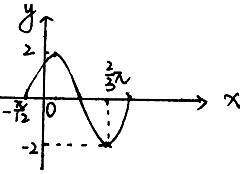 若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示
若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示