题目内容
19.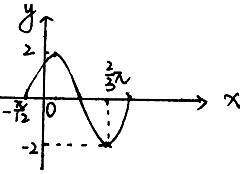 若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示
若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示(1)求f(x)的解析式
(2)若方程f(x)=m在x∈[0,$\frac{π}{2}$]有且只有一个实根,求m的取值范围.
分析 (1)由图象可以直接得到A,$\frac{3}{4}$T,代入周期公式求得ω,然后再由五点作图的第一个点可得φ得值,则函数的解析式可求.
(2)由已知可求2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],利用正弦函数的图象和性质可得sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],数形结合可求实数m的取值范围.
解答 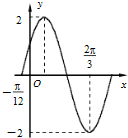 解:(1)由图可知,A=2,$\frac{3}{4}$T=$\frac{2π}{3}$-(-$\frac{π}{12}$)=$\frac{3π}{4}$,
解:(1)由图可知,A=2,$\frac{3}{4}$T=$\frac{2π}{3}$-(-$\frac{π}{12}$)=$\frac{3π}{4}$,
∴T=π,即$\frac{2π}{ω}$=π,解得:ω=2.
由五点作图的第一个点可得:2×(-$\frac{π}{12}$)+φ=0,解得:φ=$\frac{π}{6}$.
∴函数的解析式为y=2sin(2x+$\frac{π}{6}$).
(2)当x∈[0,$\frac{π}{2}$]时,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],可得f(x)=2sin(2x+$\frac{π}{6}$)∈[-1,2],
在坐标系中画出y=2sin(2x+$\frac{π}{6}$)的图象与y=m的图象,图象只有一个交点,
由图可得:m=2或m∈[-1,1).
点评 本题考查由y=Asin(ωx+φ)的部分图象求函数解析式,考查数形结合求出函数的图象的交点与方程的根的关系,考查计算能力,是中档题.

练习册系列答案
相关题目
16.某地最近十年对某商品的需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量y与年份x之间的回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)预测该地2018年的商品需求量(结果保留整数).
| 年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
| 需要量(万件) | 236 | 246 | 257 | 276 | 286 |
(2)预测该地2018年的商品需求量(结果保留整数).
17.若函数f(x)=(x+1)2-alnx在区间(0,+∞)内任取有两个不相等的实数x1,x2,不等式$\frac{{f({{x_1}+1})-f({{x_2}+1})}}{{{x_1}-{x_2}}}$>1恒成立,则a的取值范围是( )
| A. | (-∞,3) | B. | (-∞,-3) | C. | (-∞,3] | D. | (-∞,-3] |
14. 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{11}{3}$ | C. | 4 | D. | $\frac{14}{3}$ |