题目内容
11.设π<α<2π,向量$\overrightarrow{a}$=(-2,1),$\overrightarrow{b}$=(sinα,2cosα),$\overrightarrow{c}$=(cosα,-2sinα).(1)若$\overrightarrow{a}$⊥$\overrightarrow{b}$,求α;
(2)若|$\overrightarrow{b}$+$\overrightarrow{c}$|=$\sqrt{3}$,求sinα+cosα的值.
分析 (1)利用数量积的运算性质即可得出;
(2)利用向量模的计算、三角函数的值的符号,即可求出答案.
解答 解:(1)$\overrightarrow{a}$=(-2,1),$\overrightarrow{b}$=(sinα,2cosα),$\overrightarrow{c}$=(cosα,-2sinα),$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴-2sinα+2cosα=0,
∴tanα=1,
∵π<α<2π,
∴α=$\frac{5}{4}$π;
(2)由|$\overrightarrow{b}$+$\overrightarrow{c}$|=$\sqrt{3}$,得|$\overrightarrow{b}$|2+|$\overrightarrow{c}$|2+$\overrightarrow{b}$$\overrightarrow{c}$=3,
∴5-6sinαcosα=3,
∴2sinαcosα=$\frac{2}{3}$,
∴sinα与cosα同号,
∵π<α<2π,
∴π<α<$\frac{3π}{2}$,
∴sinα<0,cosα<0,
∴sinα+cosα<0,
∴(sinα+cosα)2=1+2sinαcosα=1+$\frac{2}{3}$=$\frac{5}{3}$,
∴sinα+cosα=-$\frac{\sqrt{15}}{3}$.
点评 本题考查了数量积的运算性质、向量的模、三角函数的值等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
3.设命题p:?x>1,x2+1>2,则¬p为( )
| A. | ?x>1,x2+1≤2 | B. | ?x>1,x2+1≤2 | C. | ?x≤1,x2+1≤2 | D. | ?x≤1,x2+1≤2 |
1.已知函数f(x)的定义域为[-1,2),则f(x-1)的定义域为( )
| A. | [-1,2) | B. | [0,3) | C. | (0,1] | D. | [-2,1) |
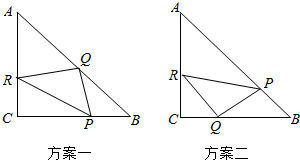 在一个直角边长为10m的等腰直角三角形ABC的草地上,铺设一个也是等腰直角三角形PQR的花地,要求P,Q,R三点分别在△ABC的三条边上,且要使△PQR的面积最小,现有两种设计方案:
在一个直角边长为10m的等腰直角三角形ABC的草地上,铺设一个也是等腰直角三角形PQR的花地,要求P,Q,R三点分别在△ABC的三条边上,且要使△PQR的面积最小,现有两种设计方案: