题目内容
18.若${({4x-\frac{1}{{\root{3}{x}}}})^n}$的展开式中各项的系数之和为729,则该展开式中x2的系数为-1280.分析 令x=1,则3n=729,解得n=6,再利用二项式定理的通项公式即可得出.
解答 解:令x=1,则3n=729,解得n=6,
∴展开式的通项公式:Tr+1=(-1)r ${C}_{6}^{r}$(4x)6-r$(\frac{1}{\root{3}{x}})^{r}$=(-1)r${C}_{6}^{r}$46-r${C}_{6}^{r}$${x}^{6-\frac{4r}{3}}$,
6-$\frac{4r}{3}$=2,解得r=3.
∴该二项式的展开式中x2项的系数为-1280.
故答案为-1280.
点评 本题考查了二项式定理的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.已知全集U=R,集合A={x|ex>1},B={x|x-3>0},则A∩B=( )
| A. | {x|x<3} | B. | {x|x>0} | C. | {x|1<x<3} | D. | {x|0<x<3} |
10.若x,y满足约束条件$\left\{\begin{array}{l}{-1≤x-y≤1}\\{2≤x+2y≤3}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.执行如图程序框图,输出的S为( )
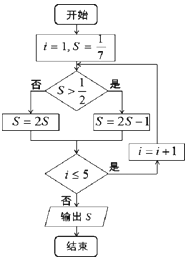

| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{6}{7}$ |
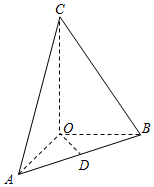 在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.
在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.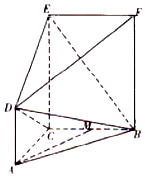 在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.
在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.