题目内容
2.已知曲线C1的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y=1+sinα}\end{array}\right.$(α为参数),以原点为极点,x轴正半轴为极轴建立极坐标系.曲线C2的极坐标方程为ρsinθ=1.(1)将曲线C1的普通方程和曲线C2的直角坐标方程;
(2)求曲线C1与曲线C2的交点的直角坐标.
分析 (1)把参数方程与极坐标方程化为直角坐标方程,求得曲线C1的普通方程x2+(y-1)2=1,由y=ρsinθ=1,曲线C2的直角坐标方程y=1;
(2)将y=1,代入得曲线C1的普通方程解方程,即可求得交点坐标.
解答 解:(1)由$\left\{\begin{array}{l}{x=cosα}\\{y=1+sinα}\end{array}\right.$,
得x2+(y-1)2=1,
曲线C1的普通方程x2+(y-1)2=1,
∵ρsinθ=1,
∴曲线C2的直角坐标方程y=1;
(2)$\left\{\begin{array}{l}{{x}^{2}+(y-1)^{2}=1}\\{y=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
直线l与圆的交点的直角坐标为(-1,1),(1,1).
点评 本题考查参数方程与普通方程的转化,将极坐标方程转化成直角坐标方程,考查直线与圆的交点问题,属于基础题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
17.(x-y)(x+y)8的展开式中x2y7的系数是( )
| A. | -20 | B. | 20 | C. | -22 | D. | 22 |
7.复数z=$\frac{-8+i}{i}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.由变量x与y相对应的一组数据(3,y1),(5,y2),(7,y3),(12,y4),(13,y5)得到的线性回归方程为$\stackrel{∧}{y}$=$\frac{1}{2}$x+20,则$\sum_{i=1}^{5}{y}_{i}$=( )
| A. | 25 | B. | 125 | C. | 120 | D. | 24 |
4.已知A(3,$\sqrt{3}$),O是坐标原点,点P(x,y)的坐标满足$\left\{\begin{array}{l}{\sqrt{3}-y≤0}\\{x-\sqrt{3}+0≥0}\\{y≥0}\end{array}\right.$,设Z为$\overrightarrow{OA}$在$\overrightarrow{OP}$上的投影,则Z的取值范围是( )
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | [-3,3] | C. | [-$\sqrt{3}$,3] | D. | [-3,$\sqrt{3}$] |
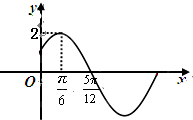 已知函数f(x)=Asin(ωx+φ)(φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(φ|<$\frac{π}{2}$)的部分图象如图所示.