题目内容
10.若函f(x)=sin2ax-sinaxcosax(a>0)的图象与直y=m(m>0)相切,并且切点的横坐标依次成公差$\frac{π}{2}$的等差数列.(Ⅰ)m的值;
(Ⅱ)若A(x0,y0)y=f(x)图象的对称中心,x0∈[0,$\frac{π}{2}$],求A的坐标.
分析 (Ⅰ)利用倍角公式降幂,然后利用两角和的正弦化积,由题意可得m为f(x)的最大值,则m的值可求;
(Ⅱ)由题意可得函数f(x)的周期为$\frac{π}{2}$,从而求得a=2,代入函数解析式,由相位的终边落在x轴上得答案.
解答 解:(Ⅰ)f(x)=sin2ax-sinaxcosax=$\frac{1-cos2ax}{2}-\frac{1}{2}sin2ax$=$-\frac{\sqrt{2}}{2}sin(2ax+\frac{π}{4})+\frac{1}{2}$,
由题意知,m为f(x)的最大值,∴m=$\frac{1+\sqrt{2}}{2}$;
(Ⅱ)由题设知,函数f(x)的周期为$\frac{π}{2}$,∴a=2,
∴$f(x)=-\frac{\sqrt{2}}{2}sin(4x+\frac{π}{4})+\frac{1}{2}$.
令$sin(4x+\frac{π}{4})=0$,得$4x+\frac{π}{4}=kπ$(k∈Z),∴$x=\frac{kπ}{4}-\frac{π}{16}$(k∈Z),
由0$≤\frac{kπ}{4}-\frac{π}{16}≤\frac{π}{2}$(k∈Z),得k=1或k=2,
因此点A的坐标为$(\frac{3π}{16},\frac{1}{2})$或$(\frac{7π}{16},\frac{1}{2})$.
点评 本题考查三角函数最值的求法,考查了三角函数的图象和性质,是基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
1.下列有关命题的说法正确的是( )
| A. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| B. | 命题“若x=y,则sin x=sin y”的逆否命题为真命题 | |
| C. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| D. | 命题“?x∈R,使得:x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” |
19.1337与382的最大公约数是( )
| A. | 191 | B. | 382 | C. | 201 | D. | 37 |
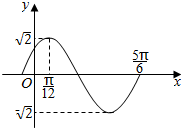 函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.