题目内容
13.已知0<a<2,复数z=a+i的模的取值范围是(1,$\sqrt{5}$).分析 求出复数的模,利用a的范围求解即可.
解答 解:∵|z|=|a+i|=$\sqrt{{a}^{2}+1}$,且0<a<2,
∴0<a2<4,∴1<a2+1<5.
∴1<|z|<$\sqrt{5}$.
故答案为:(1,$\sqrt{5}$).
点评 本题考查复数的模的求法,二次函数的性质的应用,考查计算能力.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
8.过抛物线y2=2px(p>0)的焦点F,且倾斜角为$\frac{π}{4}$的直线与抛物线交于A,B两点,若AB的垂直平分线经过点(0,2),M为抛物线上的一个动点,则M到直线11:5x-4y+4=0和l2:x=-$\frac{2}{5}$的距离之和的最小值为( )
| A. | $\frac{6\sqrt{41}}{41}$ | B. | $\frac{6\sqrt{31}}{31}$ | C. | $\frac{3\sqrt{41}}{41}$ | D. | $\frac{3\sqrt{31}}{31}$ |
5.设α、β、γ是不同的平面,m,n是不同的直线,则由下列条件能得出m⊥β的是( )
| A. | n⊥α,n⊥β,m⊥α | B. | α∩β=m,α⊥β,β⊥γ | C. | m⊥n,n?β | D. | α⊥β,α∩β=n,m⊥n |
2.设复数z1,z2在复平面内的点关于实轴对称,z1=1+i,则$\frac{z_1}{z_2}$=( )
| A. | -i | B. | i | C. | -1 | D. | 1 |
3.若p=$\sqrt{a+4}$+$\sqrt{a+5}$,q=$\sqrt{a+3}$+$\sqrt{a+6}$(a≥0),则p、q的大小关系是( )
| A. | p<q | B. | p=q | C. | p>q | D. | 由a的取值确定 |
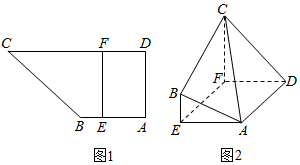 如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2.
如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2.