题目内容
12.曲线C上的动点M到定点F(1,0)的距离和它到定直线x=3的距离之比是1:$\sqrt{3}$.(Ⅰ)求曲线C的方程;
(Ⅱ)过点F(1,0)的直线l与C交于A,B两点,当△ABO面积为$\frac{2\sqrt{6}}{5}$时,求直线l的方程.
分析 (Ⅰ)设M(x,y),运用两点的距离公式和点到直线的距离公式,化简整理即可得到所求方程;
(Ⅱ)当l斜率不存在时,l方程为x=1,求得A,B的坐标,以及△ABO的面积;由直线l斜率存在,设l方程为y=k(x-1),代入椭圆方程,运用韦达定理和弦长公式,以及点到直线的距离公式,解方程可得斜率k,进而得到所求直线的方程.
解答 解:(Ⅰ)设M(x,y)
由题意可得,$\frac{{\sqrt{{{(x-1)}^2}+{y^2}}}}{|x-3|}=\frac{1}{{\sqrt{3}}}$,
整理得$\frac{x^2}{3}+\frac{y^2}{2}=1$,
则曲线C的方程为$\frac{x^2}{3}+\frac{y^2}{2}=1$;
(Ⅱ)当l斜率不存在时,l方程为x=1,
此时l与C的交点分别为$A(1,\frac{{2\sqrt{3}}}{3})$,$B(1,-\frac{{2\sqrt{3}}}{3})$,
即有$|AB|=\frac{{4\sqrt{3}}}{3}$,
则${S_{△ABO}}=\frac{1}{2}×1×\frac{{4\sqrt{3}}}{3}=\frac{{2\sqrt{3}}}{3}≠\frac{{2\sqrt{6}}}{5}$,
由直线l斜率存在,设l方程为y=k(x-1),
由$\left\{\begin{array}{l}y=k(x-1)\\ \frac{x^2}{3}+\frac{y^2}{2}=1\end{array}\right.⇒(2+3{k^2}){x^2}-6{k^2}x+3{k^2}-6=0$,
得${x_1}+{x_2}=\frac{{6{k^2}}}{{2+3{k^2}}}$,${x_1}•{x_2}=\frac{{3{k^2}-6}}{{2+3{k^2}}}$,
∴$|AB|=\sqrt{(1+{k^2})[{{(\frac{{6{k^2}}}{{2+3{k^2}}})}^2}-4\frac{{3{k^2}-6}}{{2+3{k^2}}}]}=4\sqrt{3}\frac{{1+{k^2}}}{{2+3{k^2}}}$.
设O到l的距离为d,则$d=\frac{|-k|}{{\sqrt{1+{k^2}}}}=\frac{|k|}{{\sqrt{1+{k^2}}}}$,
∴${S_{△ABO}}=\frac{1}{2}×\frac{|k|}{{\sqrt{1+{k^2}}}}×4\sqrt{3}\frac{{1+{k^2}}}{{2+3{k^2}}}=2\sqrt{3}\sqrt{\frac{{{k^2}(1+{k^2})}}{{{{(2+3{k^2})}^2}}}}=\frac{{2\sqrt{6}}}{5}$,
解得k=±1.
综上所述,当△ABO面积为$\frac{{2\sqrt{6}}}{5}$时,l的方程为y=x-1或y=-x+1.
点评 本题考查轨迹方程的求法,注意运用坐标法,考查直线方程和椭圆方程联立,运用韦达定理和弦长公式,考查运算能力,属于中档题.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | 5,15,10 | B. | 3,18,9 | C. | 7,13,10 | D. | 5,12,9 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 物理学家和数学家牛顿曾提出了物体在常温环境下温度变化的冷却模型,如果物体的初始温度为θ1℃,空气温度为θ0℃,则tmin后物体的温度f(t)满足:f(t)=θ0+(θ1-θ0)•e-kt(其中k为正的常数,e=2.71828…为自然对数的底数),现有65℃的物体,放在15℃的空气中冷却,5min以后物体的温度是45℃.
物理学家和数学家牛顿曾提出了物体在常温环境下温度变化的冷却模型,如果物体的初始温度为θ1℃,空气温度为θ0℃,则tmin后物体的温度f(t)满足:f(t)=θ0+(θ1-θ0)•e-kt(其中k为正的常数,e=2.71828…为自然对数的底数),现有65℃的物体,放在15℃的空气中冷却,5min以后物体的温度是45℃.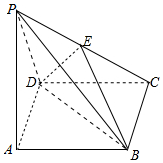 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,PD⊥CD,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,PD⊥CD,E为PC的中点.