题目内容
11.已知函数y=f(1-x)的图象如图,则y=|f(x+2)|的图象是( )
| A. | 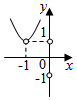 | B. |  | C. | 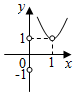 | D. | 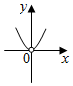 |
分析 根据函数图象的变换规律依次作出f(-x),f(x),f(x+2),|f(x+2)|的函数图象,或者根据函数的定义域进行判断.
解答 解:解法一:(1)把函数y=f(1-x)的图象向左平移1个单位得y=f(-x)的图象,
(2)作出f(-x)关于y轴对称的函数图象得y=f(x)的图象,
(3)将f(x)向左平移2个单位得y=f(x+2)的图象,
(4)将y=f(x+2)的图象在x轴下方的部分关于x轴对称上去得到|f(x+2)|的图象.
解法二:由f(1-x)的图象可知f(1-x)的定义域为x≠0,∴1-x≠1,
∴f(x)的定义域为x≠1.
令x+2≠1得x≠-1.
∴|f(x+2)|的图象在x=-1处无意义.
故选A.
点评 本题考查了函数的图象变换,熟练掌握变换规律是关键,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
1.设等比数列{an}的各项均为正数,且${a_1}=\frac{1}{2},{a_4}^2=4{a_2}•{a_8}$,若$\frac{1}{b_n}={log_2}{a_1}+{log_2}{a_2}+…+{log_2}{a_n}$,则数列{bn}的前10项和为( )
| A. | $-\frac{20}{11}$ | B. | $\frac{20}{11}$ | C. | $-\frac{9}{5}$ | D. | $\frac{9}{5}$ |
6.“a≠1”是“a2≠1”的( )
| A. | 充分不必条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.有6人入住某家庭旅馆的6个不同房间,其中的一楼有两个房间,二楼有两个房间,三楼有两个房间,若每人随机地入住这6个房间中的一个房间,则其中的甲乙两人恰好在同一楼层的两个房间的概率为( )
| A. | $\frac{5}{12}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{11}{24}$ |
20.已知点(a,$\frac{1}{3}$)在幂函数f(x)=(a2-6a+10)xb的图象上,则函数f(x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 定义域内的减函数 | D. | 定义域内的增函数 |
 如图,缉私船在A处测出某走私船在方位角为45°,距离为10海里的C处,并测得走私船正沿方位角165°的方向以9海里/时的速度沿直线方向航行.我缉私船立即以v海里/时的速度沿直线方向前去截获.
如图,缉私船在A处测出某走私船在方位角为45°,距离为10海里的C处,并测得走私船正沿方位角165°的方向以9海里/时的速度沿直线方向航行.我缉私船立即以v海里/时的速度沿直线方向前去截获.