题目内容
11. 如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别在x轴y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是( )
如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别在x轴y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是( )| A. | $\sqrt{5}$ | B. | 5 | C. | 6 | D. | 7 |
分析 设A(a,0),D(0,b),∠BAX=θ,利用AD=1得出a,b之间的关系,用a,b,θ表示出B,C的坐标,代入数量积公式运算得出关于θ的三角函数,利用三角函数的性质求出最大值.
解答 解:设A(a,0),D(0,b),∠BAX=θ,则B(a+2cosθ,2sinθ),C(2cosθ,b+2sinθ).
∵AD=1,∴a2+b2=1.
$\overrightarrow{OB}•\overrightarrow{OC}$=2cosθ(a+2cosθ)+2sinθ(b+2sinθ)=4+2acosθ+2bsinθ=4+$\sqrt{4{a}^{2}+4{b}^{2}}$sin(θ+φ)=4+2sin(θ+φ).
∴$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是4+2=6.
故选:C.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
6.已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{3}}$是不共面的三个向量,则λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$是λ2+μ2+v2=0的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
5.函数$f(x)=\sqrt{x+1}-\frac{x}{2-x}$的定义域为( )
| A. | {x|x≥-1} | B. | {x|x≠2} | C. | [-1,2)∪(2,+∞) | D. | (-1,2) |
2.已知函数$f(x)=\left\{\begin{array}{l}2-|x|,x≤2\\{({x-2})^2},x>2\end{array}\right.$,函数$g(x)=\frac{b}{2}-f(2-x)$,其中b∈R,若函数y=f(x)-g(x)恰有4个零点,则b的取值范围是( )
| A. | $(\frac{7}{8},+∞)$ | B. | $(\frac{7}{4},2)$ | C. | $(\frac{7}{8},1)$ | D. | $(\frac{7}{2},4)$ |
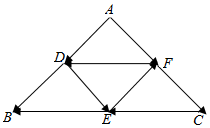 如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.
如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.