题目内容
12. 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为$(\frac{{\sqrt{5}-1}}{2},1)$.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为$(\frac{{\sqrt{5}-1}}{2},1)$.
分析 ${k}_{1}={k}_{{B}_{1}{F}_{2}}$=$\frac{b}{c}$,${k}_{2}={k}_{{A}_{2}{B}_{2}}$=-$\frac{b}{a}$.由于∠B1PA2为钝角,可得tan∠B1PA2=$\frac{{k}_{2}-{k}_{1}}{1+{k}_{1}{k}_{2}}$<0,化简整理即可得出.
解答 解:${k}_{1}={k}_{{B}_{1}{F}_{2}}$=$\frac{b}{c}$,${k}_{2}={k}_{{A}_{2}{B}_{2}}$=-$\frac{b}{a}$.
∵∠B1PA2为钝角,
∴tan∠B1PA2=$\frac{{k}_{2}-{k}_{1}}{1+{k}_{1}{k}_{2}}$=$\frac{-\frac{b}{a}-\frac{b}{c}}{1+(-\frac{b}{a})•\frac{b}{c}}$<0,
化为:ac-b2<0,
∴c2+ac-a2<0,
∴e2+e-1<0,0<e<1,
解得$\frac{\sqrt{5}-1}{2}$<e<1.
则此椭圆的离心率的取值范围为 $(\frac{{\sqrt{5}-1}}{2},1)$.
故答案为:$(\frac{{\sqrt{5}-1}}{2},1)$.
点评 本题考查了椭圆的标准方程及其性质、一元二次不等式的解法、“到角公式”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
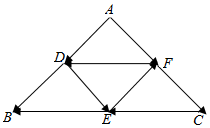 如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.
如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.