题目内容
10.已知直线l上有三点A,B,P,若$\overrightarrow{AB}$=3$\overrightarrow{BP}$且$\overrightarrow{AP}$=$λ\overrightarrow{PB}$,求λ的值.分析 根据向量加法的几何意义便可得到$\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{BP}$,进行向量的数乘运算便可得到$\overrightarrow{AB}=-(λ+1)\overrightarrow{BP}$,从而有-(λ+1)=3,这便可解出λ的值.
解答 解:$\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{BP}=λ\overrightarrow{PB}$;
∴$\overrightarrow{AB}=-(λ+1)\overrightarrow{BP}$;
又$\overrightarrow{AB}=3\overrightarrow{BP}$;
∴-(λ+1)=3;
∴λ=-4.
点评 考查向量加法及数乘的几何意义,以及向量的数乘运算,平面向量基本定理.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
18.公差不为零的等差数列{an}中,a7=2a5,则数列{an}中与4a5的值相等的项是( )
| A. | a11 | B. | a12 | C. | a13 | D. | a14 |
2.已知函数$f(x)=\left\{\begin{array}{l}2-|x|,x≤2\\{({x-2})^2},x>2\end{array}\right.$,函数$g(x)=\frac{b}{2}-f(2-x)$,其中b∈R,若函数y=f(x)-g(x)恰有4个零点,则b的取值范围是( )
| A. | $(\frac{7}{8},+∞)$ | B. | $(\frac{7}{4},2)$ | C. | $(\frac{7}{8},1)$ | D. | $(\frac{7}{2},4)$ |
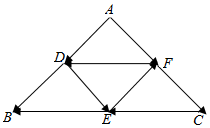 如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.
如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.