题目内容
8. 已知椭圆的中心在原点O,对称轴为坐标轴,过焦点F且与长轴垂直的直线与椭圆交于A,B两点.若OA⊥OB,试求椭圆的离心率.
已知椭圆的中心在原点O,对称轴为坐标轴,过焦点F且与长轴垂直的直线与椭圆交于A,B两点.若OA⊥OB,试求椭圆的离心率.
分析 不妨设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F(c,0).把x=c代入椭圆方程可得A$(c,\frac{{b}^{2}}{a})$,B$(c,-\frac{{b}^{2}}{a})$.由于OA⊥OB,可得$\overrightarrow{OA}•\overrightarrow{OB}$=0,化简解出即可.
解答 解:不妨设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F(c,0).
把x=c代入椭圆方程可得:${y}^{2}={b}^{2}(1-\frac{{c}^{2}}{{a}^{2}})$=$\frac{{b}^{4}}{{a}^{2}}$,解得$y=±\frac{{b}^{2}}{a}$.
取A$(c,\frac{{b}^{2}}{a})$,B$(c,-\frac{{b}^{2}}{a})$.
∵OA⊥OB,
∴$\overrightarrow{OA}•\overrightarrow{OB}$=${c}^{2}-\frac{{b}^{4}}{{a}^{2}}$=0,
化为ac-(a2-c2)=0,
∴e2+e-1=0,0<e<1,
解得e=$\frac{\sqrt{5}-1}{2}$.
∴椭圆的离心率为$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了直线与椭圆相交问题、椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.设f(x)为奇函数,且在(0,+∞)上是增函数,f(-2015)=0,则xf(x)>0的解集为( )
| A. | (-∞,2015)∪(2015,+∞) | B. | (-∞,-2015)∪(0,2015) | C. | (-2015,0)∪(0,2015) | D. | (-2015,0)∪(2015,+∞) |
18.已知集合A={x|y=$\sqrt{3x-{x}^{2}}$},B={x|$\frac{x+1}{x-2}$<0},则A∩B=( )
| A. | {x|0<x<2} | B. | {x|0≤x<2} | C. | {x|-1<x≤3} | D. | {x|2<x≤3} |
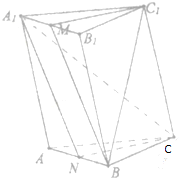 在三棱柱ABC-A1B1C1中,上下两个底面平行,侧面是平行四边形,N是AB的中点,M是A1B1的中点,求证:平面A1NC∥平面BMC1.
在三棱柱ABC-A1B1C1中,上下两个底面平行,侧面是平行四边形,N是AB的中点,M是A1B1的中点,求证:平面A1NC∥平面BMC1.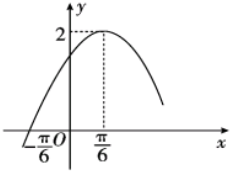 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.