题目内容
18．已知集合A={x|y=$\sqrt{3x-{x}^{2}}$}，B={x|$\frac{x+1}{x-2}$＜0}，则A∩B=（ ）| A． | {x|0＜x＜2} | B． | {x|0≤x＜2} | C． | {x|-1＜x≤3} | D． | {x|2＜x≤3} |
分析 根据集合A，B的表示，分别解3x-x2≥0，$\frac{x+1}{x-2}＜0$即可得出集合A，B，然后求交集即可．
解答 解：解3x-x2≥0得，0≤x≤3；
∴A={x|0≤x≤3}；
解$\frac{x+1}{x-2}＜0$得，-1＜x＜2；
∴B={x|-1＜x＜2}；
∴A∩B={x|0≤x＜2}．
故选：B．
点评 考查描述法表示集合，解一元二次不等式和分式不等式，以及交集的运算．
练习册系列答案
黄冈创优卷系列答案
相关题目
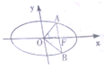已知椭圆的中心在原点O，对称轴为坐标轴，过焦点F且与长轴垂直的直线与椭圆交于A，B两点．若OA⊥OB，试求椭圆的离心率．
3．函数y=x2-1和y=1-x2的图象关于（ ）
| A． | 坐标原点对称 | B． | x轴对称 | C． | y轴对称 | D． | 直线x+y=0对称 |