题目内容
19.已知双曲线的渐近线方程为y=±$\sqrt{2}$x,焦点坐标为(-$\sqrt{6}$,0)($\sqrt{6}$,0),则双曲线方程为$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{4}=1$.分析 由题意,c=$\sqrt{6}$,$\frac{b}{a}$=$\sqrt{2}$,可得a=$\sqrt{2}$,b=2,即可求出双曲线方程.
解答 解:由题意,c=$\sqrt{6}$,$\frac{b}{a}$=$\sqrt{2}$,
∴a=$\sqrt{2}$,b=2,
∴双曲线方程为$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{4}=1$.
故答案为:$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{4}=1$.
点评 本题考查双曲线的方程与性质,确定几何量是关键.

练习册系列答案
相关题目
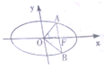 已知椭圆的中心在原点O,对称轴为坐标轴,过焦点F且与长轴垂直的直线与椭圆交于A,B两点.若OA⊥OB,试求椭圆的离心率.
已知椭圆的中心在原点O,对称轴为坐标轴,过焦点F且与长轴垂直的直线与椭圆交于A,B两点.若OA⊥OB,试求椭圆的离心率.