题目内容
20.设f(x)为奇函数,且在(0,+∞)上是增函数,f(-2015)=0,则xf(x)>0的解集为( )| A. | (-∞,2015)∪(2015,+∞) | B. | (-∞,-2015)∪(0,2015) | C. | (-2015,0)∪(0,2015) | D. | (-2015,0)∪(2015,+∞) |
分析 若xf(x)>0,则对应f(x)的图象在第一,三象限,结合已知,画出函数的草图,可得答案.
解答 解:∵f(x)为奇函数,且在(0,+∞)上是增函数,
∴f(x)在(-∞,0)上也是增函数,
又由f(-2015)=0,故f(2015)=0,
则f(x)的图象如下图所示: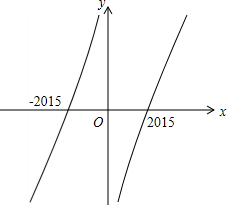
若xf(x)>0,则对应f(x)的图象在第一,三象限,
故x∈(-∞,2015)∪(2015,+∞),
故选:A
点评 本题考查的往右点是函数的奇偶性和函数的单调性,抽象不等式的解法,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知函数f(x)满足:对于任意的x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2)-2015,且当x>0时,有f(x)<2015.若f(x)在[-2015,2015]上的最大值、最小值分别为M、N,则M+N的值为( )
| A. | 2014 | B. | 2015 | C. | 4028 | D. | 4030 |
12.解一元二次不等式2x2-4x+3≥0时,可先考虑以下哪个二次函数( )
| A. | y=2x2-3x+4 | B. | y=2x2+3x+4 | C. | y=2x2-4x+3 | D. | y=x2+4x+3 |
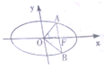 已知椭圆的中心在原点O,对称轴为坐标轴,过焦点F且与长轴垂直的直线与椭圆交于A,B两点.若OA⊥OB,试求椭圆的离心率.
已知椭圆的中心在原点O,对称轴为坐标轴,过焦点F且与长轴垂直的直线与椭圆交于A,B两点.若OA⊥OB,试求椭圆的离心率.