题目内容
10.已知向量$\overrightarrow a=(cos(\frac{π}{2}+x),sin(\frac{π}{2}+x))$,$\overrightarrow b=(-sinx,\sqrt{3}sinx)$,f(x)=$\overrightarrow a•\overrightarrow b$.(1)求函数f(x)的最小正周期及f(x)的最大值;
(2)在锐角三角形ABC中,角A,B,C的对边分别为a,b,c,若f($\frac{A}{2}$)=1,a=2$\sqrt{3}$,求三角形ABC面积的最大值.
分析 (1)利用两个向量的数量积公式,三角恒等变换,化简函数的解析式,利用正弦函数的周期性以及最值,从而求得函数f(x)的最小正周期及f(x)的最大值.
(2)利用余弦定理以及基本不等式,求得三角形ABC面积的最大值.
解答 解:(1)易得$\overrightarrow a=(-sinx,cosx)$,
则f(x)=$\overrightarrow a•\overrightarrow b={sin^2}x+\sqrt{3}sinxcosx$=$\frac{1}{2}$-$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$.
∴f(x)的最小正周期T=$\frac{2π}{2}$=π,当$2x-\frac{π}{6}=\frac{π}{2}+2kπ,k∈Z$时,
即$x=\frac{π}{3}+kπ,(k∈Z)$,f(x)取最大值$\frac{3}{2}$.
(2)锐角三角形ABC中,∵f($\frac{A}{2}$)=sin(A-$\frac{π}{6}$)+$\frac{1}{2}$=1,
∴sin(A-$\frac{π}{6}$)=$\frac{1}{2}$,∴A=$\frac{π}{3}$.
∵a2=b2+c2-2bccosA,∴12=b2+c2-bc,
∴b2+c2=12+bc≥2bc,∴bc≤12.(当且仅当b=c时等号成立)
∴S=$\frac{1}{2}$bc•sinA=$\frac{\sqrt{3}}{4}$bc≤3$\sqrt{3}$.
∴当三角形ABC为等边三解形时面积的取最大值是3$\sqrt{3}$.
点评 本题主要考查两个向量的数量积公式,三角恒等变换,正弦函数的周期性以及最值,余弦定理以及基本不等式的应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案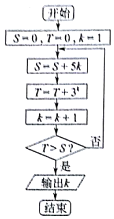
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| 班级 | 1 | 2 | 3 | 4 | 5 |
| 数学(x分) | 111 | 113 | 119 | 125 | 127 |
| 物理(y分) | 92 | 93 | 96 | 99 | 100 |
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
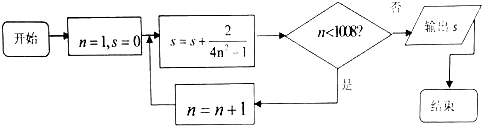
| A. | 1 | B. | $\frac{2018}{2019}$ | C. | $\frac{2018}{2017}$ | D. | $\frac{2016}{2017}$ |
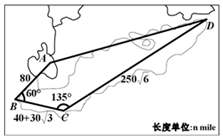 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.